
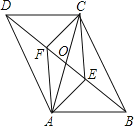
【题目】如图,在四边形ABCD中,∠B=∠D=90°,∠C=60°,AD=1,BC=2,求AB、CD的长.

【答案】AB=2![]() -2,CD=4-
-2,CD=4-![]() .
.
【解析】
此题为几何题,看题目只是一个四边形,要求两条未知边,那肯定要添辅助线.过点D作DH⊥BA延长线于H,作DM⊥BC于M.构建矩形HBMD.利用矩形的性质和解直角三角形来求AB、CD的长度.
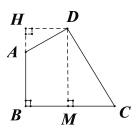
如图,过点D作DH⊥BA延长线于H,作DM⊥BC于点M.
∵∠B=90°,
∴四边形HBMD是矩形.
∴HD=BM,BH=MD,∠ABM=∠ADC=90°,
又∵∠C=60°,
∴∠ADH=∠MDC=30°,
∴在Rt△AHD中,AD=1,∠ADH=30°,则AH=![]() AD=
AD=![]() ,DH=
,DH=![]() .
.
∴MC=BC-BM=BC-DH=2-![]() =
=![]() .
.
∴在Rt△CMD中,CD=2MC=4-![]() ,DM=
,DM=![]() CD=
CD=![]() .
.
∴AB=BH-AH=DM-AH=![]() -
-![]() =
=![]()


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ABC=90°,CD⊥BC,BD与AC相交于点E,AB=9,BC=4,DC=3.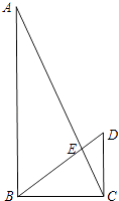
(1)求BE的长度;
(2)求△ABE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图甲,点C将线段AB分成两部分(AC>BC),如果 ![]() =
= ![]() ,那么称点C为线段AB的黄金分割点.某数学兴趣小组在进行课题研究时,由黄金分割点联想到“黄金分割线”,类似地给出“黄金分割线”的定义:直线l将一个面积为S的图形分成面积分别为S1 , S2(S1>S2)的两部分,如果
,那么称点C为线段AB的黄金分割点.某数学兴趣小组在进行课题研究时,由黄金分割点联想到“黄金分割线”,类似地给出“黄金分割线”的定义:直线l将一个面积为S的图形分成面积分别为S1 , S2(S1>S2)的两部分,如果 ![]() =
= ![]() ,那么称直线l为该图形的黄金分割线.
,那么称直线l为该图形的黄金分割线.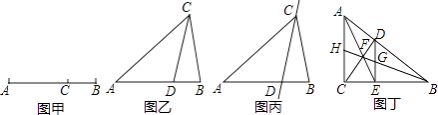
(1)如图乙,在△ABC中,∠A=36°,AB=AC,∠ACB的平分线交AB于点D,请问点D是否是AB边上的黄金分割点,并证明你的结论;
(2)若△ABC在(1)的条件下,如图丙,请问直线CD是不是△ABC的黄金分割线,并证明你的结论;
(3)如图丁,在Rt△ABC中,∠ACB=90°,D为斜边AB上的一点,(不与A,B重合)过D作DE⊥BC于点E,连接AE,CD相交于点F,连接BF并延长,与DE,AC分别交于点G,H.请问直线BH是直角三角形ABC的黄金分割线吗?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有甲、乙两个不透明的布袋,甲袋中装有3个完全相同的小球,分别标有数字0,1,2;乙袋中装有2个完全相同的小球,分别标有数字﹣1,﹣2.现从甲袋中随机抽取一个小球,将标有的数字记录为x,再从乙袋中随机抽取一个小球,将标有的数字记录为y,确定点M的坐标为(x,y).
(1)用树状图或列表法列举点M所有可能的坐标;
(2)求点M(x,y)在二次函数y=x2﹣2x﹣2的图象上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC⊥BC于C,CD⊥AB于D,点E在AC上,EF⊥AB于F,且∠1=∠2.
(1)试判断CD与EF是否平行并说明理由.
(2)试判断DG与BC是否垂直并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为A(-4,5),C(-1,3).
(1)请在如图所示的网格内作出x轴、y轴;
(2)请作出△ABC关于y轴对称的△A1B1C1;
(3)写出点B1的坐标并求出△A1B1C1的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.若AB=8,AD=6 ![]() ,AF=4
,AF=4 ![]() ,则AE的长为 .
,则AE的长为 . 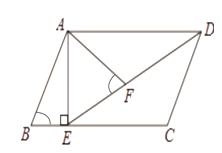
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AB=CD,对角线AC,BD相交于点O,AE⊥BD于点E,CF⊥BD于点F,连接AF,CE,若DE=BF,则下列结论:①CF=AE;②OE=OF;③四边形ABCD是平行四边形;④图中共有四对全等三角形.其中正确结论的个数是
A.4 B.3 C.2 D.1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com