
【题目】对于平面直角坐标系xOy中的点![]() ,若点
,若点![]() 的坐标为
的坐标为![]() (其中k为常数,且
(其中k为常数,且![]() ),则称点
),则称点![]() 为点P的“k属派生点”.
为点P的“k属派生点”.
例如:![]() 的“4属派生点”为
的“4属派生点”为![]() ,即
,即![]() .
.
(1)点![]() 的“2属派生点”
的“2属派生点”![]() 的坐标为________;
的坐标为________;
(2)若点P的“3属派生点”![]() 的坐标为
的坐标为![]() ,求点P的坐标;
,求点P的坐标;
(3)若点P在y轴的正半轴上,点P的“k属派生点”为![]() 点,且点
点,且点![]() 到y轴的距离不小于线段OP长度的5倍,则k的取值范围是________________.
到y轴的距离不小于线段OP长度的5倍,则k的取值范围是________________.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或![]()
【解析】
(1)根据“k属派生点”的概念计算;
(2)设点P的坐标为(x,y),根据“k属派生点”的概念列出方程组,解方程组得到答案;
(3)设点P的坐标为(0,b),根据“k属派生点”的概念求出P′点的坐标,根据题意列出不等式,解不等式得到答案.
(1)(1)点P(-2,3)的“2属派生点”P′的坐标为(-2+2×3,3-2×2),即(4,-1),
故答案为:(4,-1);
(2)设P点为![]() 根据题意
根据题意![]()
解得![]()
则点P的坐标为![]()
(3)设点P的坐标为(0,b),
则点P的“k属派生点”P′点的坐标为(kb,b),
由题意得,|kb|≥5b,
当k>0时,k≥5,
当k<0时,k≤-5,
则k的取值范围是k≥5或k≤-5,
故答案为: ![]() 或
或![]() .
.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,点D、E分别在AB、AC上,BE与CD相交于点O,已知∠B=∠C,现添加下面的哪一个条件后,仍不能判定△ABE≌△ACD( )
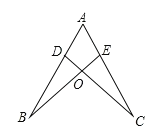
A. AD=AEB. AB=AC
C. BE=CDD. ∠AEB=∠ADC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某市城区地图(比例尺1∶9000)上,新安大街的图上长度与光华大街的图上长度分别是16 cm,10 cm.
(1)新安大街与光华大街的实际长度各是多少米?
(2)新安大街与光华大街的图上长度之比是多少?它们的实际长度之比呢?你发现了什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(a,3),点C(5,c),点B的纵坐标为6且横纵坐标互为相反数,直线AC![]() 轴,直线CB
轴,直线CB![]() 轴:
轴:
(1)写出A、B、C三点坐标;
(2)求△ABC的面积;
(3)若P为线段OB上动点且点P的横、纵坐标互为相反数,当△BCP的面积大于12小于16时,求点P横坐标取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了更好地开展“阳光体育一小时”活动,对本校学生进行了“写出你最喜欢的体育活动项目(只写一项)”的随机抽样调查,下面是根据得到的相关数据绘制的统计图的一部分.
抽样调查学生最喜欢的运动项目的人数统计图 各运动项目的喜欢人数占抽样总人数百分比统计图

请根据以上信息解答下列问题:
(1)该校对________名学生进行了抽样调查;
(2)请将图1和图2补充完整;
(3)图2中跳绳所在的扇形对应的圆心角的度数是________;
(4)若该校共有2400名同学,请利用样本数据估计全校学生中最喜欢跳绳运动的人数约为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() ,点B在直线MN上,点A为直线PQ上一动点,连接AB.在直线AB的上方做
,点B在直线MN上,点A为直线PQ上一动点,连接AB.在直线AB的上方做![]() ,使
,使![]() ,设
,设![]() ,
,![]() 的平分线所在直线交PQ于点D.
的平分线所在直线交PQ于点D.
(1)如图1,若![]() ,且点C恰好落在直线MN上,则
,且点C恰好落在直线MN上,则![]() ________;
________;
(2)如图2,若![]() ,且点C在直线MN右侧,求
,且点C在直线MN右侧,求![]() 的度数;
的度数;
(3)若点C在直线MN的左侧,求![]() 的度数.(用含有α的式子表示)
的度数.(用含有α的式子表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知平面直角坐标系内两点A、B,点![]() ,点B与点A关于y轴对称.
,点B与点A关于y轴对称.
(1)则点B的坐标为________;
(2)动点P、Q分别从A点、B点同时出发,沿直线AB向右运动,同向而行,点P的速度是每秒4个单位长度,点Q的速度是每秒2个单位长度,设P、Q的运动时间为t秒,用含t的代数式表示![]() 的面积S,并写出t的取值范围;
的面积S,并写出t的取值范围;
(3)在平面直角坐标系中存在一点![]() ,满足
,满足![]() .求m的取值范围.
.求m的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AB∥CD,EF交AB于E,交CD于F,∠AEF=68°,FG平分∠EFD,KF⊥FG,求∠KFC的度数.

解:∵AB∥CD(已知)
∴∠EFD=∠AEF( )
∵∠AEF=68°(已知)
∴∠EFD=∠AEF=68°( )
∵FG平分∠EFD(已知)
所以∠EFG=∠GFD=![]() ∠EFD=34°( )
∠EFD=34°( )
又因为KF⊥FG( )
所以∠KFG=90°( )
所以∠KFC=180°-∠GFD-∠KFG= .
查看答案和解析>>
科目:初中数学 来源: 题型:
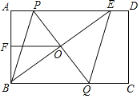
【题目】如图,在矩形ABCD中,E是AD上一点,PQ垂直平分BE,分别交AD,BE,BC于点P,O,Q,连接BP,EQ.
(1)求证:四边形BPEQ是菱形;
(2)F为AB的中点,则线段OF与线段AE有什么位置关系和数量关系,并说明理由;
(3)在(2)的条件下,若AB=6,OF=4,求PQ的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com