
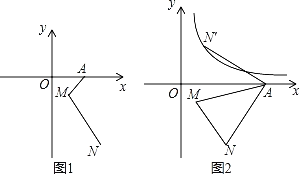
【题目】在平面直角坐标系xOy中,点A(a,0)为x轴上一动点,点M(1,﹣1)、点N(3,﹣4),连接AM、MN,点N关于直线AM的对称点为N′.
(1)若a=2,在图1中画出线段MN关于直线AM的对称图形MN′(保留作图痕迹),直接写出点N′的坐标 ;
(2)若a>0,连接AN、AN′,当点A运动到∠N′AN=90°时,点N′恰好在双曲线y=![]() 上(如图2),求k的值;
上(如图2),求k的值;
(3)点A在x轴上运动,若∠N′MN=90°,此时a的值为 .
【答案】(1)(﹣2,1);(2)20;(3)﹣4或![]()
【解析】
(1)根据要求画出图形,利用图象法解决问题即可.
(2)如图2,过A,M分别作y轴平行线BE,CD,过N,N′分别作x轴平行线,交BE,CD于点D,B,C.利用全等三角形的性质解决问题即可.
(3)画出图形,利用图象法解决问题.
解:(1)作图如图1所示,N′(﹣2,1).
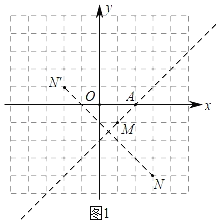
故答案为(﹣2,1).
(2)如图2,过A,M分别作y轴平行线BE,CD,过N,N′分别作x轴平行线,交BE,CD于点D,B,C.
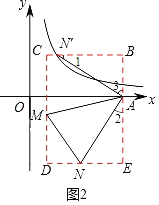
∴∠B=∠E=∠D=∠C=90°,
∴∠1+∠3=90°,
∵∠N’AN=90°,
∴∠2+∠3=90°,
∴∠1=∠2
又AN′=AN,
∴△ABN≌△NEA(AAS),
∴BA=EN,BN=EA
∵A(a,0),M(1,﹣1),N(3,﹣4),
∴BA=EN=a﹣3,BN′=EA=4,DM=2,DM=3,
N′(a﹣4,a﹣3),由轴对称性质可知MN′=MN=![]() ,
,
∴NC=a﹣4﹣1=a=5,CM=a=3﹣(﹣1)=a﹣2
CN2+CM2=MN2=13,
∴(a﹣5)2+(a﹣2)2=13,
∴a2﹣7a﹣8=0,
∴k=(a﹣4)(a﹣3)=a2﹣7a+12=(a2﹣7a﹣8)+20=20.
故答案为:20;
(3)如下图中,
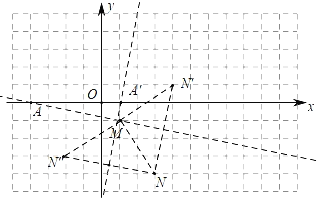
将线段MN绕点M逆时针旋转90°得到N′(4,1),作线段NN′的垂直平分线交x轴于A,
∴直线NN′的解析式为y=5x﹣19,
∴线段NN′的中垂线的解析式为![]() ,可得A(﹣4,0).
,可得A(﹣4,0).
将线段MN绕点M顺时针旋转90°得到N″(﹣2,﹣3),作线段N″N′的垂直平分线交x轴于A′,同法可得直线y=5x﹣6,
∴A′(![]() ,0).
,0).
∴a=﹣4或![]() .
.
故答案为﹣4或![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .直线
.直线![]() 经过点
经过点![]() 、
、![]() .
.
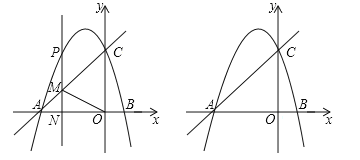
(1)求抛物线的解析式;
(2)![]() 是抛物线上一动点,过
是抛物线上一动点,过![]() 作
作![]() 轴交直线
轴交直线![]() 于点
于点![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() .
.
①若以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形,求
为顶点的四边形是平行四边形,求![]() 的值.
的值.
②当射线![]() 、
、![]() 、
、![]() 中一条射线平分另外两条射线的夹角时,直接写出
中一条射线平分另外两条射线的夹角时,直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是半圆O的直径,射线AM⊥AB,点P在AM上,连接OP交半圆O于点D,PC切半圆O于点C,连接BC,OC.
(1)求证:△OAP≌△OCP;
(2)若半圆O的半径等于2,填空:
①当AP= 时,四边形OAPC是正方形;
②当AP= 时,四边形BODC是菱形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋里面有13个完全相同的小球,在每一个小球上书写一个汉字,这些汉字组成一句话:“知之为知之,不知为不知,是知也”.随机摸出一个小球然后放回,再随机摸取一个小球,两次取出的小球都是“知”的概率是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
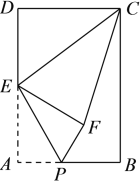
【题目】如图,在矩形ABCD中,AB=4,AD=6,点E为AD的中点,点P为线段AB上一个动点,连接EP,将△APE沿EP折叠得到△EPF,连接CE,CF,当△ECF为直角三角形时,AP的长为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
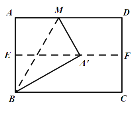
【题目】如图,对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展平,再一次折叠纸片,使点A落在EF上的点A′处,并使折痕经过点B,得到折痕BM,若矩形纸片的宽AB=4,则折痕BM的长为( )
A.![]() B.
B.![]() C.8D.
C.8D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() 、
、![]() 两点,点
两点,点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
(1)![]() _________,
_________,![]() _________;
_________;
(2)如图1,![]() 是
是![]() 轴上一动点,点
轴上一动点,点![]() 在
在![]() 轴上,连接
轴上,连接![]() ,求
,求![]() 的最小值;
的最小值;
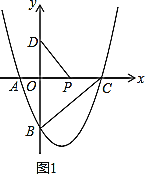
(3)如图2,点![]() 在抛物线上,若
在抛物线上,若![]() ,求点
,求点![]() 的坐标.
的坐标.
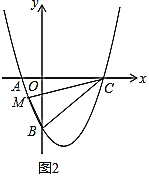
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋中有标号为1,2,3,4的四个小球,除数字不同外,小球没有任何区别,摸球前先搅拌均匀,每次摸一个球
(1)摸出一个球,摸到标号为偶数的概率为 .
(2)从袋中不放回地摸两次,用列表或树状图求出两球标号数字为一奇一偶的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com