
【题目】在解决数学问题的过程中,我们常用到“分类讨论”的数学思想,下面是运用分类讨论的数学思想解决问题的过程,请仔细阅读,并解答问题.
(提出问题)三个有理数![]() 、
、![]() 、
、![]() 满足
满足![]() ,求
,求![]() 的值.
的值.
(解决问题)
解:由题意,得![]() 、
、![]() 、
、![]() 三个有理数都为正数或其中一个为正数,另两个为负数,
三个有理数都为正数或其中一个为正数,另两个为负数,
①![]() 、
、![]() 、
、![]() 都是正数,即
都是正数,即![]() 、
、![]() 、
、![]() 时,则
时,则![]() :
:
②当![]() 、
、![]() 、
、![]() 中有一个为正数,另两个为负数时,不妨设
中有一个为正数,另两个为负数时,不妨设![]() 、
、![]() 、
、![]() ,则,
,则,![]() ,综上所述,
,综上所述,![]() 值为
值为![]() 或
或![]() .
.
(探究)请根据上面的解题思路解答下面的问题:
(1)三个有理数![]() 、
、![]() 、
、![]() 满足
满足![]() ,求
,求![]() 的值;
的值;
(2)若![]() 、
、![]() 、
、![]() 为三个不为
为三个不为![]() 的有理数,且
的有理数,且![]() ,求
,求![]() 的值.
的值.
科目:初中数学 来源: 题型:
【题目】一快递员需要在规定时间内开车将快递送到某地,若快递员开车每分钟行驶1.2![]() ,就早到10分钟;若快递员开车每分钟行驶0.8
,就早到10分钟;若快递员开车每分钟行驶0.8![]() ,就要迟到5分钟.试求出规定时间及快递员所行驶的总路程.
,就要迟到5分钟.试求出规定时间及快递员所行驶的总路程.
小明和小新在解答时先设出未知数,然后列出方程如下:
![]() ①,
①,![]() ②,其中方程①由小明所列,方程②由小新所列.
②,其中方程①由小明所列,方程②由小新所列.
(1)小明所设![]() 表示 ;
表示 ;
小新所设![]() 表示 .
表示 .
(2)请选小明或小新的方法写出完整的解答过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中:
①0是最小的整数;
②有理数不是正数就是负数;
③正整数、负整数、正分数、负分数统称为有理数;
④非负数就是正数;
⑤![]() 不仅是有理数,而且是分数;
不仅是有理数,而且是分数;
⑥![]() 是无限不循环小数,所以不是有理数;
是无限不循环小数,所以不是有理数;
⑦无限小数不都是有理数;
⑧正数中没有最小的数,负数中没有最大的数.
其中错误的说法的个数为( )
A.7个B.6个C.5个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,按以下步骤作图:①以A为圆心,任意长为半径作弧,分别交AB,AD于点M,N;②分别以M,N为圆心,以大于![]() MN的长为半径作弧,两弧相交于点P;③作AP射线,交边CD于点Q,若DQ=2QC,BC=3,则平行四边形ABCD周长为________.
MN的长为半径作弧,两弧相交于点P;③作AP射线,交边CD于点Q,若DQ=2QC,BC=3,则平行四边形ABCD周长为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线a、b分别与∠A的两边相交,且a∥b.下列各角的度数关系正确的是( )
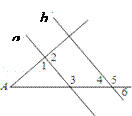
A. ∠2+∠5>180° B. ∠2+∠3<180° C. ∠1+∠6>180° D. ∠3+∠4<180°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)![]() 克糖水中有
克糖水中有![]() 克糖(
克糖(![]() >
>![]() >0),则糖的质量与糖水的质量比为_______;若再添加
>0),则糖的质量与糖水的质量比为_______;若再添加![]() 克糖,并全部溶解(
克糖,并全部溶解(![]() >0),则糖的质量与糖水的质量比为__________;生活常识告诉我们,添加的糖完全溶解后,糖水会更甜,因此我们可以猜想出以上两个质量比之间的大小关系是______________;
>0),则糖的质量与糖水的质量比为__________;生活常识告诉我们,添加的糖完全溶解后,糖水会更甜,因此我们可以猜想出以上两个质量比之间的大小关系是______________;
(2)我们的猜想正确吗?请你证明这个猜想。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB=10,P是线段AB上的动点,分别以AP、PB为边在线段AB的同侧作等边△ACP和△PDB,连接CD,设CD的中点为G,当点P从点A运动到点B时,则点G移动路径的长是_________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,M是△ABC的边BC的中点,AN平分![]() ,BN
,BN![]() AN于点N,延长BN交AC于点D,已知AB=10,AC=16.
AN于点N,延长BN交AC于点D,已知AB=10,AC=16.

(1)求证:BN=DN;
(2)求MN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示为一个污水净化塔内部,污水从上方入口进入后,流经形如等腰直角三角形的净化材枓表面,流向如图中箭头所示,每一次水流流经三角形两腰的机会相同,经过四层净化后流入底部的5个出口中的一个.下列判断:①5个出口的出水量相同;②2号出口的出水量与4号出口的出水量相同;③1,2,3号出水口的出水量之比约为1:4:6;④若净化材枓损耗的速度与流经其表面水的数量成正比,则更换最慢的一个三角形材枓使用的时间约为更换最快的一个三角形材枓使用时间的8倍.其中正确的判断有( )个.

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com