
【题目】如图,在△ABC中,∠ACB=90°,点D、E分别是AC、AB的中点,点F在BC的延长线上,且∠CDF=∠A.
(1)求证:四边形DECF是平行四边形;
(2)若∠A=30°,写出图中所有与FD长度相等的线段.
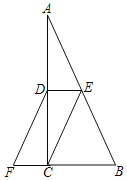
【答案】(1)见解析;(2)AE=EB=BC=EC=DF
【解析】
(1)首先利用三角形中位线的性质得出DE∥BC,进而结合直角三角形的性质得出CE=![]() AB=AE,得出∠CDF=∠ACE,推出DF∥CE,再利用平行四边形的定义判定即可.
AB=AE,得出∠CDF=∠ACE,推出DF∥CE,再利用平行四边形的定义判定即可.
(2)只要证明△EBC是等边三角形即可判定;
(1)证明:∵D,E分别为AC,AB的中点,
∴DE为△ACB的中位线,
∴DE//BC.
∵CE为Rt△ACB的斜边上的中线,
∴CE=![]() AB=AE.
AB=AE.
∴∠A=∠ACE.
又∵∠CDF=∠A,
∴∠CDF=∠ACE.
∴DF//CE.
又∵DE//BC,
∴四边形DECF为平行四边形.
(2)解:图中所有与FD长度相等的线段有:AE、BE、CE、BC;理由如下:
∵∠A=30°,∠ACB=90°,
∴∠B=60°,
∵EC=EA=EB,
∴△EBC是等边三角形,
∴AE=EB=BC=EC=DF.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:初中数学 来源: 题型:
【题目】已知关于![]() 的代数式
的代数式![]() ,设代数式
,设代数式![]() 的值
的值![]() .
.
下表中列出了当![]() 分别取-1,0,1,2,3,4,5,…,
分别取-1,0,1,2,3,4,5,…,![]() ,
,![]() ,…时对应的
,…时对应的![]() 值.
值.
| … | -1 | 0 | 1 | 2 | 3 | 4 | 5 | … |
|
| … |
| … | 10 | 5 | 2 | 1 | 2 | 5 |
| … |
|
| … |
(1)表中![]() 的值为 ;
的值为 ;
(2)当![]() 时,
时,![]() 有最小值,最小值是 ;
有最小值,最小值是 ;
(3)比较![]() 与
与![]() 的大小.
的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的益智玩具由一块主板AB和一个支撑架CD组成,其侧面示意图如图1所示,测得AB⊥BD,AB=40cm,CD=25cm,链接点C为AB的中点,现为了方便儿童操作,须调整玩具的摆放,将AB绕点B顺时针旋转,CD绕点C旋转同时点D做水平滑动,如图2,当点C1到BD的距离为10cm时停止,求点D滑动的距离和点A经过的路径的长.(结果保留整数,参考数据:![]() ≈1.732,
≈1.732,![]() ≈4.583,π,3.141,可使用科学计算器)
≈4.583,π,3.141,可使用科学计算器)
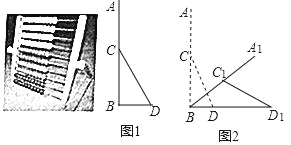
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在边长为![]() 个单位长度的小正方形网格中,有
个单位长度的小正方形网格中,有![]() (顶点是网格线的交点).
(顶点是网格线的交点).

(![]() )画出
)画出![]() 关于直线
关于直线![]() 对称的图形
对称的图形![]() ;再将
;再将![]() 向下平移
向下平移![]() 个单位,画出平移后得到的
个单位,画出平移后得到的![]() .
.
(2)计算出△ABC的面积
(3)在直线![]() 上画出点
上画出点![]() ,使
,使![]() 最小.
最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形纸片ABCD中,AB=6cm,AD=8cm,折叠该纸片,使得AB边落在对角线AC上,点B落在点F处,折痕为AE,则EF=_____cm.
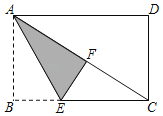
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,四边形ABCD中,∠ABC=∠ADC=90°,AD=CD.
(1)求证:BD平分∠ABC;
(2)如图2,点E、F分别在AB、BC上,连接EF,M是EF的中点,过M作EF的垂线交BD于P.求证:AE+CF=![]() PD;
PD;
(3)如图3,在(2)条件下,连AF,若AE=CF,∠DAF=2∠AFE=2α,AF=13,BC=12![]() ,(BC>AB).求BD的长.
,(BC>AB).求BD的长.
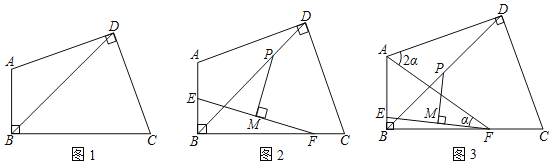
查看答案和解析>>
科目:初中数学 来源: 题型:
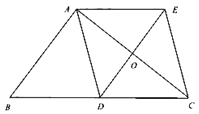
【题目】证明题:本题须有完整过程,需要括号中的理由,只限本学期所学
如图,在![]() 中,
中,![]() 是边
是边![]() 上的中线,
上的中线,![]() ,
,![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,连接
,连接![]() .
.
(1)求证:![]() ;
;
(2)若![]() ,求证:四边形
,求证:四边形![]() 是菱形.
是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某青春党支部在精准扶贫活动中,给结对帮扶的贫困家庭赠送甲、乙两种树苗让其栽种.已知乙种树苗的价格比甲种树苗贵10元,用480元购买乙种树苗的棵数恰好与用360元购买甲种树苗的棵数相同.
(1)求甲、乙两种树苗每棵的价格各是多少元?
(2)在实际帮扶中,他们决定再次购买甲、乙两种树苗共50棵,此时,甲种树苗的售价比第一次购买时降低了10%,乙种树苗的售价不变,如果再次购买两种树苗的总费用不超过1500元,那么他们最多可购买多少棵乙种树苗?
查看答案和解析>>
科目:初中数学 来源: 题型:
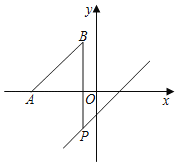
【题目】如图,在平面直角坐标系xOy中,点B(﹣1,3),点A(﹣5,0),点P是直线y=x﹣2上一点,且∠ABP=45°,则点P的坐标为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com