
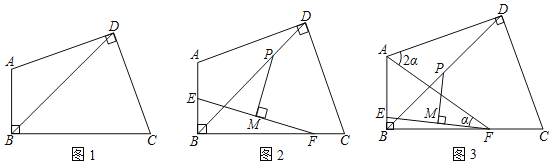
【题目】如图1,四边形ABCD中,∠ABC=∠ADC=90°,AD=CD.
(1)求证:BD平分∠ABC;
(2)如图2,点E、F分别在AB、BC上,连接EF,M是EF的中点,过M作EF的垂线交BD于P.求证:AE+CF=![]() PD;
PD;
(3)如图3,在(2)条件下,连AF,若AE=CF,∠DAF=2∠AFE=2α,AF=13,BC=12![]() ,(BC>AB).求BD的长.
,(BC>AB).求BD的长.
【答案】(1)见解析;(2)见解析;(3)17
【解析】
(1)作DG⊥BC于G,DH⊥BA于H,通过证明△DAH≌△DCG可证点D到BA和BC的距离相等;
(2)PM是中垂线,因此连接PE、PF,有PE=PF,由第(1)问可知∠ABD=∠CBD,则B、E、P、F四点共圆,推出∠EPF是直角,将△BEP绕点P逆时针旋转90°至△NFP,可以得出BE+BF=![]() BP,注意四边形ABCD的结构与四边形PEBF结构一样,因此同理可得AB+BC=
BP,注意四边形ABCD的结构与四边形PEBF结构一样,因此同理可得AB+BC=![]() BD,进而得出所证结论.
BD,进而得出所证结论.
(3)由于AE=CF,因此可以考虑CF为边在BC上方构造△QCF≌△FEA,连接AQ、AC.可以推出△AFQ是等腰直角三角形,同时注意△ACD也是等腰直角三角形,∠CAQ是两个45°的重叠角,于是∠CAQ=90﹣2α,然后可推出AC=AQ,而AQ=![]() AF=13
AF=13![]() ,BC已知,由勾股定理可算出AB长度,根据第(2)问中的结论,BD长度就自然得出.
,BC已知,由勾股定理可算出AB长度,根据第(2)问中的结论,BD长度就自然得出.
解:(1)如图1,作DG⊥BC于G,DH⊥BA于H.
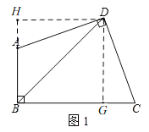
则∠DHA=∠DGC=90°.
∵∠ABC=∠ADC=90°,
∴∠BAD+∠BCD=180°,
∵∠BAD+∠DAH=180°,
∴∠DAH=∠DCG,
在△DAH和△DCG中:
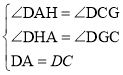 ,
,
∴△DAH≌△DCG(AAS),
∴DH=DG,
∴BD平分∠ABC.
(2)如图2,连接PE、PF,
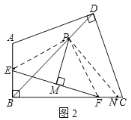
∵M为EF中点且PM⊥EF,
∴PE=PF,
∵∠EBP=∠FBP,
∴P、E、B、F四点共圆,
∴∠PEB+∠PFB=∠EBF+∠EPF=180°,
∴∠EBF=90°,
∴∠EPF=90°,
在FC上截取FN=BE,连接PN.
∴∠PFN+∠PFB=180°,
∴∠PFN=∠PEB,
在△PEB和△PFN中:
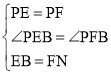 ,
,
∴△PEB≌△PFN(SAS),
∴PB=PN,∠EPB=∠FPN
∴∠BPN=∠BPF+∠FPN=∠BPF+∠EPB=∠EPF=90°,
∴△BPN是等腰直角三角形,
∴BN=![]() BP,
BP,
∵BN=BF+FN=BF+BE,
∴BE+BF=![]() BP,
BP,
同理可证BA+BC=![]() BD,
BD,
∴AE+BE+BF+FC=![]() (BP+PD)=
(BP+PD)=![]() BP+
BP+![]() PD,
PD,
∴AE+CF=![]() PD.
PD.
(3)如图3,作△QCF≌△FEA,连接AQ、AC.
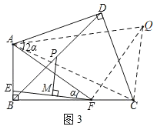
则∠EAF=∠CFQ,AF=FQ,∠FQC=∠AFE=α,
∵∠EAF+∠AFB=90°,
∴∠CFQ+∠AFB=90°,
∴∠AFQ=90°,
∴△AFQ是等腰直角三角形,
∴AQ=![]() AF=13
AF=13![]() ,∠FAQ=∠FQA=45°,
,∠FAQ=∠FQA=45°,
∵AD=DC,∠ADC=90°,
∴△ADC是等腰直角三角形,
∴∠DAC=∠DCA=45°,
∴∠DAC+∠FAQ=∠DAF+∠QAC=90°,
∴∠QAC=90°﹣∠DAC=90°﹣2α,
∵∠AQC=∠AQF+∠FQC=45°+α,
∴∠ACQ=180°﹣∠QAC﹣∠AQC=45°+α,
∴AC=AQ=13![]() ,
,
∵BC=12![]() ,
,
∴AB=5![]() ,
,
由(2)可知AB+BC=![]() BD,
BD,
∴BD=![]() (AB+BC)=17.
(AB+BC)=17.


科目:初中数学 来源: 题型:
【题目】如图,菱形OABC的一边OA在x轴的负半轴上,O是坐标原点,tan∠AOC=![]() ,反比例函数y=
,反比例函数y=![]() 的图象经过点C,与AB交于点D,若△COD的面积为16,则k的值等于_____.
的图象经过点C,与AB交于点D,若△COD的面积为16,则k的值等于_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于一次函数y=x+6,下列结论错误的是( )
A. 函数值随自变量增大而增大 B. 函数图像与![]() 轴正方向成45°角
轴正方向成45°角
C. 函数图像不经过第四象限 D. 函数图像与![]() 轴交点坐标是(0,6)
轴交点坐标是(0,6)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具商店销售功能相同的两种品牌的计算器,购买2个A品牌和3个B品牌的计算器共需156元;购买3个A品牌和1个B品牌的计算器共需122元。
(1)求这两种品牌计算器的单价;
(2)学校开学前夕,该商店对这两种计算器开展了促销活动,具体办法如下:A品牌计算器按原价的八折销售,B品牌计算器5个以上超出部分按原价的七折销售。设购买个x个A品牌的计算器需要y1元,购买x个B品牌的计算器需要y2元,分别求出y1、y2关于x的函数关系式;
(3)小明准备联系一部分同学集体购买同一品牌的计算器,若购买计算器的数量超过5个,购买哪种品牌的计算器更合算?请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
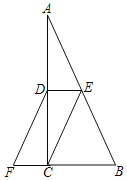
【题目】如图,在△ABC中,∠ACB=90°,点D、E分别是AC、AB的中点,点F在BC的延长线上,且∠CDF=∠A.
(1)求证:四边形DECF是平行四边形;
(2)若∠A=30°,写出图中所有与FD长度相等的线段.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“足球运球”是中考体育必考项目之一.兰州市某学校为了解今年九年级学生足球运球的掌握情况,随机抽取部分九年级学生足球运球的测试成绩作为一个样本,按A,B,C,D四个等级进行统计,制成了如下不完整的统计图.(说明:A级:8分﹣10分,B级:7分﹣7.9分,C级:6分﹣6.9分,D级:1分﹣5.9分)
根据所给信息,解答以下问题:
(1)在扇形统计图中,C对应的扇形的圆心角是 度;
(2)补全条形统计图;
(3)所抽取学生的足球运球测试成绩的中位数会落在 等级;
(4)该校九年级有300名学生,请估计足球运球测试成绩达到A级的学生有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
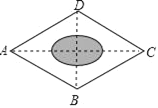
【题目】如图,为测量平地上一块不规则区域(图中的阴影部分)的面积,画一个对角线为AC和BD的菱形,使不规则区域落在菱形内,其中AC=8m,BD=4m,现向菱形内随机投掷小石子(假设小石子落在菱形内每一点都是等可能的),经过大量重复投掷试验,发现小石子落在不规则区域的频率稳定在常数25%,由此可估计不规则区域的面积是_____m2.
查看答案和解析>>
科目:初中数学 来源: 题型:
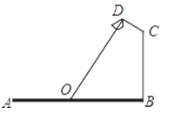
【题目】如图,要在宽为22米的大道两边安装路灯,路灯的灯臂CD长2米,且与灯柱BC成120°角,路灯采用圆锥形灯罩,灯罩的轴线DO与灯臂CD垂直,当灯罩的轴线DO通过公路路面的中心线时照明效果最佳,求路灯的灯柱BC高度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com