
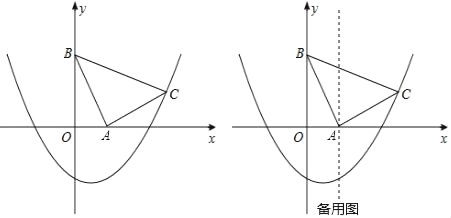
【题目】如图,在平面直角坐标系xOy中,△ABC是等腰直角三角形,∠BAC=90°,A(1,0),B(0,2),二次函数y=![]() x2+bx﹣2的图象经过C点.
x2+bx﹣2的图象经过C点.
(1)求二次函数的解析式;
(2)平移该二次函数图象的对称轴所在直线l,若直线l恰好将△ABC的面积分为1:2两部分,请求出此时直线l与x轴的交点坐标;
(3)将△ABC以AC所在直线为对称轴翻折180°,得到△AB′C,那么在二次函数图象上是否存在点P,使△PB′C是以B′C为直角边的直角三角形?若存在,请求出P点坐标;若不存在,请说明理由.
【答案】(1)y=![]() x2-
x2-![]() x﹣2;(2)直线l与x轴的交点坐标为(1,0)或(3﹣
x﹣2;(2)直线l与x轴的交点坐标为(1,0)或(3﹣![]() ,0);(3)点P的坐标为:(﹣
,0);(3)点P的坐标为:(﹣![]() ,
,![]() )或(﹣1,﹣1)或(
)或(﹣1,﹣1)或(![]() ,﹣
,﹣![]() ).
).
【解析】
(1)过点C作CD⊥x轴于点D,根据△AOB≌△CDA求出CD、OD得出C(3,1),再代入抛物线![]() 即可.
即可.
(2)先求出S△ABC,求出直线BC的解析式为![]() ,同理求得直线AC、AB的解析式,设直线l与x轴交点坐标为(x,0),设直线l与BC、AC分别交于点F、E,根据
,同理求得直线AC、AB的解析式,设直线l与x轴交点坐标为(x,0),设直线l与BC、AC分别交于点F、E,根据![]() ,得出
,得出![]() ,求出x即可,设直线l与BC、AB分别交于点F、E,根据
,求出x即可,设直线l与BC、AB分别交于点F、E,根据![]() ,得出
,得出![]() 求出x即可.
求出x即可.
(3)延长CB交抛物线于点P3,过点B′作B′P1⊥BC,交抛物线于点P1、P2,设直线B′P1的解析式为:![]() ,过点B′作B′M⊥x轴于点M,根据△AOB≌△AMB′求出B′的坐标,得出直线B′P1的解析式为:
,过点B′作B′M⊥x轴于点M,根据△AOB≌△AMB′求出B′的坐标,得出直线B′P1的解析式为:![]() ,再根据
,再根据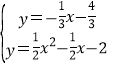 得出P1、P2的坐标,根据
得出P1、P2的坐标,根据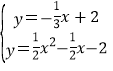 得出P3的坐标.
得出P3的坐标.
解:(1)如图1所示,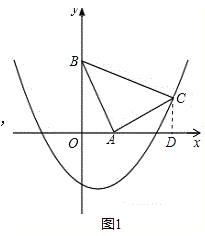
过点C作CD⊥x轴于点D,则∠CAD+∠ACD=90°.
∵△ABC是等腰直角三角形,
∴AB=AC,∠BAC=90°,
∴∠OAB+∠CAD=90°,
∴∠OAB=∠ACD,
∵∠BOA=∠ADC=90°,
在△AOB和△CDA中,
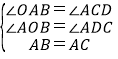 ,
,
∴△AOB≌△CDA(AAS).
∴CD=OA=1,AD=OB=2,
∴OD=OA+AD=3,
∴C(3,1).
∵点C(3,1)在抛物线![]() ,
,
∴![]() 解得:b=
解得:b=![]() ,
,
∴抛物线的解析式为:![]() .
.
(2)在Rt△AOB中,
∵OA=1,OB=2,
∴AB=![]() ,
,
∴![]() .
.
设直线BC的解析式为y=kx+b,
∵B(0,2),C(3,1),
∴![]() ,
,
解得k=![]() ,b=2,
,b=2,
∴![]() .
.
同理求得直线AC的解析式为:![]() ,
,
直线AB的解析式为:y=-2x+2,
设直线l与x轴交点坐标为(x,0)
如图2:设直线l与BC、AC分别交于点F、E,则EF=![]() .
.
△CEF中,EF边上的高h=OD-x=3-x.
由题意得:![]() ,
,
即:![]() ,
,
∴![]() ,
,
解得x1=![]() ,x2=
,x2=![]() (不合题意,舍去),
(不合题意,舍去),
如图3: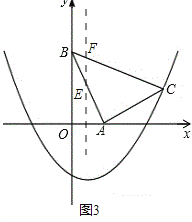
设直线l与BC、AB分别交于点F、E,
则EF=![]()
△BEF中,EF边上的高h=x.
由题意得:![]() .
.
即:![]() .
.
解得x1=1,x2=-1(不合题意,舍去)
当直线l与x轴交点坐标为(1,0)或(![]() ,0)时,恰好将△ABC的面积分为1:2的两部分,
,0)时,恰好将△ABC的面积分为1:2的两部分,
(3)存在.
如图4,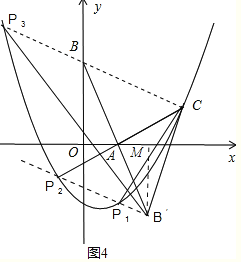
延长CB交抛物线于点P3,过点B′作B′P1⊥BC,交抛物线于点P1、P2,
则CB∥B′P1,
设直线B′P1的解析式为:![]() ,
,
过点B′作B′M⊥x轴于点M,
在△AOB和△AMB′中,
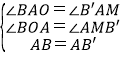 ,
,
∴△AOB≌△AMB′(AAS),
∴B′M=BO=2,
AM=AO=1,
∴B′的坐标为(2,-2),
∴![]() ,
,
∴b=![]() ,
,
∴直线B′P1的解析式为:y=![]()
由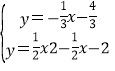 得
得![]() 或
或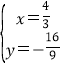 ,
,
∴P1的坐标是(-1,-1),P2的坐标是![]() ,
,
∵∠ACB=∠ACB′=45°,
∴∠B′CP3=90°,
由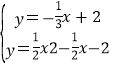 得:
得:![]() (舍去),或
(舍去),或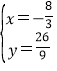 ,
,
∴P3的坐标是![]() ,
,
∴P点坐标是P1(-1,-1),P2![]() ,P3
,P3![]() .
.


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:初中数学 来源: 题型:
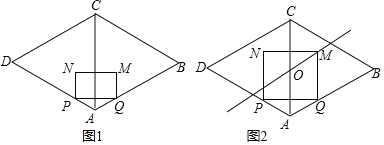
【题目】如图①,在菱形![]() 中,
中,![]() ,
,![]() .点
.点![]() 从点
从点![]() 出发以每秒2个单位的速度沿边
出发以每秒2个单位的速度沿边![]() 向终点
向终点![]() 运动,过点
运动,过点![]() 作
作![]() 交边
交边![]() 于点
于点![]() ,过点
,过点![]() 向上作
向上作![]() ,且
,且![]() ,以
,以![]() 、
、![]() 为边作矩形
为边作矩形![]() .设点
.设点![]() 的运动时间为
的运动时间为![]() (秒),矩形
(秒),矩形![]() 与菱形
与菱形![]() 重叠部分图形的面积为
重叠部分图形的面积为![]() .
.
(1)用含![]() 的代数式表示线段
的代数式表示线段![]() 的长.
的长.
(2)当点![]() 落在边
落在边![]() 上时,求
上时,求![]() 的值.
的值.
(3)当![]() 时,求
时,求![]() 与
与![]() 之间的函数关系式,
之间的函数关系式,
(4)如图②,若点![]() 是
是![]() 的中点,作直线
的中点,作直线![]() .当直线
.当直线![]() 将矩形
将矩形![]() 分成两部分图形的面积比为
分成两部分图形的面积比为![]() 时,直接写出
时,直接写出![]() 的值
的值
查看答案和解析>>
科目:初中数学 来源: 题型:
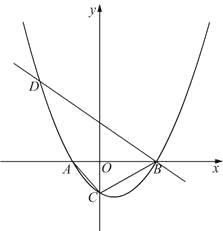
【题目】如图,已知抛物线![]() (
(![]() 为常数,且
为常数,且![]() )与
)与![]() 轴从左至右依次交于A,B两点,与
轴从左至右依次交于A,B两点,与![]() 轴交于点C,经过点B的直线
轴交于点C,经过点B的直线![]() 与抛物线的另一交点为D.
与抛物线的另一交点为D.
(1)若点D的横坐标为-5,求抛物线的函数表达式;
(2)若在第一象限的抛物线上有点P,使得以A,B,P为顶点的三角形与△ABC相似,求![]() 的值;
的值;
(3)在(1)的条件下,设F为线段BD上一点(不含端点),连接AF,一动点M从点A出发,沿线段AF以每秒1个单位的速度运动到F,再沿线段FD以每秒2个单位的速度运动到D后停止. 当点F的坐标是多少时,点M在整个运动过程中用时最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂甲、乙两个部门各有员工400人,为了解这两个部门员工的生产技能情况,进行了抽样调查,过程如下,请补充完整.
收集数据
从甲、乙两个部门各随机抽取20名员工,进行了生产技能测试,测试成绩(百分制)如下:
甲 78 86 74 81 75 76 87 70 75 90
75 79 81 70 74 80 86 69 83 77
乙 93 73 88 81 72 81 94 83 77 83
80 81 70 81 73 78 82 80 70 40
整理、描述数据
按如下分数段整理、描述这两组样本数据:
成绩 人数 部门 | 40≤x≤49 | 50≤x≤59 | 60≤x≤69 | 70≤x≤79 | 80≤x≤89 | 90≤x≤100 |
甲 | 0 | 0 | 1 | 11 | 7 | 1 |
乙 |
(说明:成绩80分及以上为生产技能优秀,70--79分为生产技能良好,60--69分为生产技能合格,60分以下为生产技能不合格)
分析数据
两组样本数据的平均数、中位数、众数如下表所示:
部门 | 平均数 | 中位数 | 众数 |
甲 | 78.3 | 77.5 | 75 |
乙 | 78 | 80.5 | 81 |
视力范围分组 | 组中值 | 频数 |
3.95≤x<4.25 | 4.1 | 20 |
4.25≤x<4.55 | 4.4 | 10 |
4.55≤x<4.85 | 4.7 | 30 |
4.85≤x<5.15 | 5.0 | 60 |
5.15≤x<5.45 | 5.3 | 30 |
合计 | 150 |
(1)分别指出参加抽测学生的视力的众数、中位数所在的范围;
(2)若视力为4.85以上(含4.85)为正常,试估计该校八年级学生视力正常的人数约为多少?
(3)根据频数分布表求加权平均数时,统计中常用各组的组中值代表各组的实际数据,把各组的频数相应组中的权.请你估计该校八年级学生的平均视力是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
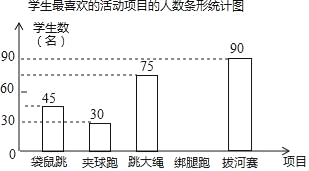
【题目】为了丰富校园文化,某校决定举行学生趣味运动会,将比赛项目确定为袋鼠跳,夹球跑,跳大绳,绑腿跑和拔河赛5项,为了解学生对这5项运动的喜欢情况,随机调查了该校部分学生最喜欢的一种项目(每名学生必选且只能选择5项中的一种),并将调查结果绘制成如图所示的不完整的统计图表:
根据图表中提供的信息解答下列问题:
(1)求a,b的值.
(2)请将条形统计图补充完整.
(3)根据调查结果,请你估计该校2500名学生中有多少名学生最喜欢绑腿跑.
学生最喜欢的活动项目的人数统计表
项目 | 学生数(名) | 百分比(%) |
袋鼠跳 | 45 | 15 |
夹球跑 | a | 10 |
跳大绳 | 75 | 25 |
绑腿跑 | b | 20 |
拔河赛 | 90 | 30 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是我国古代数学的经典著作,书中有一个问题:“今有黄金九枚,白银一十一枚,称之重适等.交易其一,金轻十三两.问金、银一枚各重几何?”.意思是:甲袋中装有黄金9枚(每枚黄金重量相同),乙袋中装有白银11枚(每枚白银重量相同),称重两袋相等.两袋互相交换1枚后,甲袋比乙袋轻了13两(袋子重量忽略不计).问黄金、白银每枚各重多少两?设每枚黄金重x两,每枚白银重y两,根据题意得( )
A. ![]()
B. ![]()
C. ![]()
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校为了提高学生跳远科目的成绩,对全校500名九年级学生开展了为期一个月的跳远科目强化训练。王老师为了了解学生的训练情况,强化训练前,随机抽取了该年级部分学生进行跳远测试,经过一个月的强化训练后,再次测得这部分学生的跳远成绩,将两次测得的成绩制作成图所示的统计图和不完整的统计表(满分10分,得分均为整数).
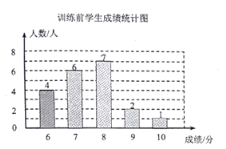
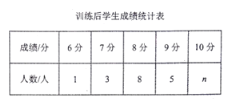
根据以上信息回答下列问题:
(1)训练后学生成绩统计表中![]() ,并补充完成下表:
,并补充完成下表:

(2)若跳远成绩9分及以上为优秀,估计该校九年级学生训练后比训练前达到优秀的人数增加了多少?
(3)经调查,经过训练后得到9分的五名同学中,有三名男生和两名女生,王老师要从这五名同学中随机抽取两名同学写出训练报告,请用列表或画树状图的方法,求所抽取的两名同学恰好是一男一女的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com