
直线y=x﹣6与x轴、y轴分别交于A、B两点,点E从B点出发,以每秒1个单位长度的速度沿线段BO向O点移动(不考虑点E与B、O两点重合的情况),过点E作EF∥AB,交x轴于点F,将四边形ABEF沿直线EF折叠后,与点A对应的点记作点C,与点B对应的点记作点D,得到四边形CDEF,设点E的运动时间为t秒.
(1)画出当t=2时,四边形ABEF沿直线EF折叠后的四边形CDEF(不写画法);
(2)在点E运动过程中,CD交x轴于点G,交y轴于点H,试探究t为何值时,△CGF的面积为 ;
;
(3)设四边形CDEF落在第一象限内的图形面积为S,求S关于t的函数解析式,并求出S的最大值.
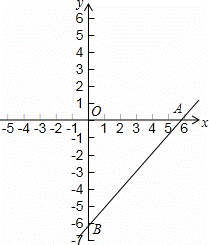
解:(1)如图1:
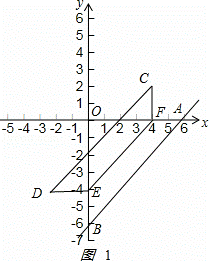
(2)如图2:
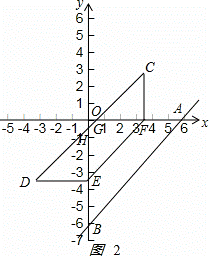 ,
,
由折叠的性质,得∠C=∠A=∠COA=45°,AF=BE=CF=t,
S△CFG=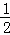 CF•FG=
CF•FG=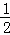 t2=
t2=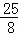 ,
,
解得t=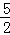 ,t=﹣
,t=﹣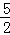 (不符合题意,舍);
(不符合题意,舍);
(3)分两种情况讨论:
①当0<t≤3时,如图2:
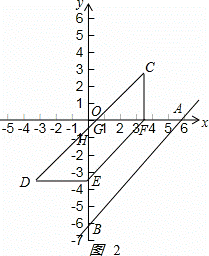
四边形DCEF落在第一象限内的图形是△DFG,
∴S=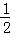 t2,
t2,
∵S=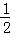 t2,在t>0时,S随t增大而增大,
t2,在t>0时,S随t增大而增大,
∴t=3时,S最大=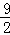 ;
;
②当3<t<6时,如图2:
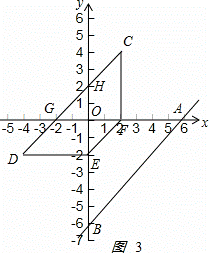 ,
,
四边形DCEF落在第一象限内的图形是四边形DHOF,
∴S四边形CHOF=S△CGF﹣S△HGO,
∴S=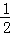 t2﹣
t2﹣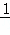 2(2t﹣6)2
2(2t﹣6)2
=﹣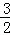 t2+12t﹣18
t2+12t﹣18
=﹣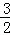 (t﹣4)2+6,
(t﹣4)2+6,
∵a=﹣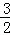 <0,
<0,
∴S有最大值,
∴当t=4时,S最大=6,
综上所述,当S=4时,S最大值为6.
点评: 本题考查了一次函数综合题,利用了轴对称的性质:成轴对称的两个图形全等,三角形的面积公式,图形割补法是求面积的重要方法,分类讨论是解题关键,以防遗漏.


科目:初中数学 来源: 题型:
一个批发商销售成本为 20元/千克的某产品,根据物价部门规定:该产品每千克售价不得超过90元,在销售过程中发现的售量y(千克)与售价x(元/千克)满足一次函数关系,对应关系如下表:
20元/千克的某产品,根据物价部门规定:该产品每千克售价不得超过90元,在销售过程中发现的售量y(千克)与售价x(元/千克)满足一次函数关系,对应关系如下表:
| 售价x(元/千克) | … | 50 | 60 | 70 | 80 | … |
| 销售量y(千克) | … | 100 | 90 | 80 | 70 | … |
(1)求y与x的函数关系式;
(2)该批发商若想获得4000元的利润,应将售价定为多少元?
(3)该产品每千克售价为多少元时,批发商获得的利润w(元)最大?此时的最大利润为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
在一个不透明的口袋装有三个完全相同的小球,分别标号为1、2、3.求下列事件的概率:
(1)从中任取一球,小球上的数字为偶数;
(2)从中任取一球,记下数字作为点A的横坐标x,把小球放回袋中,再从中任取一球记下数字作为点A的纵坐标y,点A(x,y)在函数y=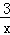 的图象上.
的图象上.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com