
如图,点P(t,0)是x轴正半轴上的一个动点,过点P作y轴的平行线,分别与直线 ,直线
,直线 交于A, B两点,以AB为边向右侧作正方形ABCD.有下列五个结论:①∠AOB=90°;②△AOB是等腰三角形;③OP2=2AP•PB ;④S△AOB=3S△AOP;⑤当
交于A, B两点,以AB为边向右侧作正方形ABCD.有下列五个结论:①∠AOB=90°;②△AOB是等腰三角形;③OP2=2AP•PB ;④S△AOB=3S△AOP;⑤当 时,正方形ABCD的周长是16,其中正确结论的序号是 .
时,正方形ABCD的周长是16,其中正确结论的序号是 .

(3)(4).
【解析】
试题分析:①由两条垂直直线的斜率的积等于﹣1即可判定①∠AOB=90°故选项错误;
②根据等腰三角形的判定定理即可判定②△AOB是等腰三角形,故选项错误;
③由直线的斜率可知 ,
, ,根据2(
,根据2( )=
)= ,即可求得OP2=2AP•PB,故选项正确;
,即可求得OP2=2AP•PB,故选项正确;
④设A(m, m),则B(m,﹣m),得出△AOP的面积=
m),则B(m,﹣m),得出△AOP的面积= OP•
OP• m=
m= m•OP,△BOP的面积=
m•OP,△BOP的面积= OP•m=
OP•m= •OP,从而求得S△BOP=2S△AOP,进而得出S△AOB=3S△AOP,故选项正确;
•OP,从而求得S△BOP=2S△AOP,进而得出S△AOB=3S△AOP,故选项正确;
⑤ 时根据直线的解析式先求得PA=1、PB=2,进而求得AB=3,所以正方形的周长=12,故选项错误;
时根据直线的解析式先求得PA=1、PB=2,进而求得AB=3,所以正方形的周长=12,故选项错误;
试题解析:①由直线 ,直线
,直线 可知,它们的斜率的积=
可知,它们的斜率的积= ,所以∠AOB≠90°,故∠AOB=90°错误;
,所以∠AOB≠90°,故∠AOB=90°错误;
②∵AB⊥x轴,∠AOP≠∠BOP,∠AOB≠90°,∴OA≠OB,OB≠AB,OA≠AB,
∴△AOB不是等腰三角形,故△AOB是等腰三角形;
③由直线的斜率可知: ,
, ,∴2(
,∴2( )=
)= ,
,
∴OP2=2AP•PB,故OP2=2AP•PB正确;
④设A(m, m),则B(m,﹣m),
m),则B(m,﹣m),
∵△AOP的面积= OP•
OP• m=
m= m•OP,△BOP的面积=
m•OP,△BOP的面积= OP•m=
OP•m= •OP,
•OP,
∴S△BOP=2S△AOP,∴S△AOB=3S△AOP,故S△AOB=3S△AOP正确;
⑤ 时,PA=
时,PA= ×2=1,PB=|﹣1×2|=2,∴AB=PA+PB=1+2=3,
×2=1,PB=|﹣1×2|=2,∴AB=PA+PB=1+2=3,
∴正方形ABCD的周长=4AB=4×3=12;故当t=2时,正方形ABCD的周长是16错误;
故答案为③④.
考点:一次函数综合题.


科目:初中数学 来源:2014-2015学年江苏省镇江市丹徒区八年级10月调研数学试卷(解析版) 题型:填空题
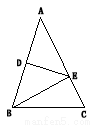
如图,在△ABC中,AC=8cm,ED垂直平分AB,如果△EBC的周长是14cm,那么BC的长度为 _ cm.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江西省上学期九年级第一次段考数学试卷(解析版) 题型:选择题
为支援雅安灾区,小慧准备通过爱心热线捐款,她只记得号码的前5位,后三位由5,1,2,这三个数字组成,但具体顺序忘记了,他第一次就拨通电话的概率是( )
A.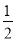 B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省靖江市共同体九年级上学期期中考试数学试卷(解析版) 题型:解答题
(本题8分) 某工厂现有80台机器,每台机器平均每天生产384件产品,现准备增加一批同类机器以提高生产总量,在试生产中发现,由于其它生产条件没变,因此每增加一台机器,每台机器平均每天将少生产4件产品.问应增加多少台机器,才可以使每天的生产总量达到30976件?
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江西省上学期九年级第一次段考数学试卷(解析版) 题型:选择题
如图,将长方形纸片ABCD折叠,使边DC落在对角线AC上,折痕为CE,且D点落在对角线D'处。若AB=3,AD=4,则ED的长为( )

A. B.3 C.1 D.
B.3 C.1 D.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江西省八年级上学期期中考试数学试卷(解析版) 题型:解答题
如图,在平行四边形ABCD中,E为BC的中点,连接DE.延长DE交AB的延长线于点F.求证:AB=BF.

查看答案和解析>>
科目:初中数学 来源:2014-2015学年江西省上学期九年级第一次段考数学试卷(解析版) 题型:解答题
(12分)如图,点P是菱形ABCD对角线AC上的一点,连接DP并延长DP交边AB于点E,连接BP并延长交边AD于点F,交CD的延长线于点G

(1)求证:△APB≌△APD;
(2)已知DF:FA=1:2,设线段DP的长为x,线段PF的长为y。
①求y与x的函数关系式;
②当x=6时,求线段FG的长。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com