
【题目】已知,如图,AB∥CD.
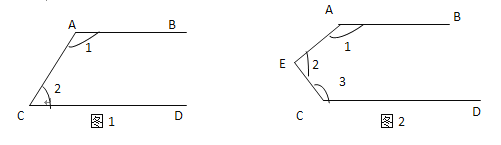
(1)则图①中的∠1+∠2的度数是180°.
(2)则图②中的∠1+∠2+∠3的度数是多少?
解:如图⑤,过点E作EF∥AB(为了解题的需要,添加的线叫做辅助线,辅助线常常画成虚线).
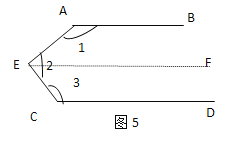
所以∠1+∠AEF=180°.
因为AB∥CD,
所以CD∥EF.
所以∠FEC+∠3=180°.
所以∠1+∠2+∠3=360°.
认真阅读(2)的解题过程,求图③中∠1+∠2+∠3+∠4的度数是多少?探究图④中∠1+∠2+∠3+∠4+…+∠n的度数是多少?
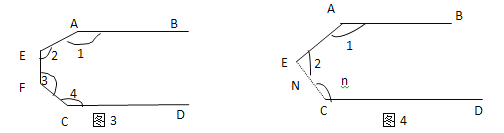
【答案】540°;(n-1)180°.
【解析】
分别过C,D作CE∥AB,DF∥AB,则CE∥DF∥CD,根据平行线的性质即可得到结论;根据角的个数n与角的和之间的关系是(n-1)180°,于是得到∠1+∠2+∠3+∠4+…+∠n的度数=(n-1)180°.
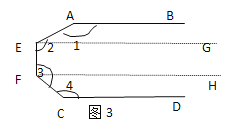
如图③,分别过E,F作GE∥AB,HF∥AB,则AB∥EG∥FH∥CD,
∴∠A+∠AEG=∠GEF+∠HFE=∠C+∠CFH=180°,
∴∠1+∠2+∠3+∠4=∠A+∠AEG+∠GEF+∠HFE+∠C+∠CFH=540°=3×180°;
由(1)(2)可得角的个数n与角的和之间的关系是(n-1)180°,
∴∠1+∠2+∠3+∠4+…+∠n的度数为(n-1)180°.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,C为线段AB延长线上一点,D为线段BC上一点,CD=2BD,E为线段AC上一点,CE=2AE,若图中所有线段的长度之和是线段AD长度的7倍,则![]() 的值为( )
的值为( )
![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,三角形ABC三边的长分别为AB=m2﹣n2,AC=2mn,BC=m2+n2,其中m、n都是正整数.以AB、AC、BC为边分别向外画正方形,面积分别为S1、S2、S3,那么S1、S2、S3之间的数量关系为_____.
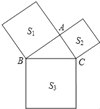
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),AB∥CD,猜想∠BPD与∠B.∠D的关系,说明理由.(提示:三角形的内角和等于180°)
①填空或填写理由
解:猜想∠BPD+∠B+∠D=360°
理由:过点P作EF∥AB,
∴∠B+∠BPE=180°______
∵AB∥CD,EF∥AB,
∴______∥_____,(如果两条直线都和第三条直线平行,那么这两条直线也互相平行)
∴∠EPD+______=180°
∴∠B+∠BPE+∠EPD+∠D=360°
∴∠B+∠BPD+∠D=360°
②依照上面的解题方法,观察图(2),已知AB∥CD,猜想图中的∠BPD与∠B.∠D的关系,并说明理由.
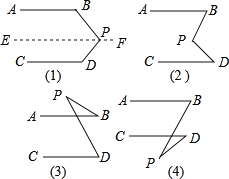
③观察图(3)和(4),已知AB∥CD,直接写出图中的∠BPD与∠B.∠D的关系,不说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC是腰长为1的等腰直角三形,以Rt△ABC的斜边AC为直角边,画第二个等腰Rt△ACD,再以Rt△ACD的斜边AD为直角边,画第三个等腰Rt△ADE,…,依此类推,则第2018个等腰直角三角形的斜边长是______.
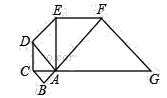
查看答案和解析>>
科目:初中数学 来源: 题型:
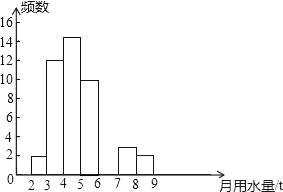
【题目】小王同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了50户居民的月均用水量(单位:t),并绘制了样本的频数分布表和频数分布直方图(如图).
月均用水量(单位:t) | 频数 | 百分比 |
2≤x<3 | 2 | 4% |
3≤x<4 | 12 | 24% |
4≤x<5 |
|
|
5≤x<6 | 10 | 20% |
6≤x<7 |
| 12% |
7≤x<8 | 3 | 6% |
8≤x<9 | 2 | 4% |
(1)请根据题中已有的信息补全频数分布表和频数分布直方图;
(2)如果家庭月均用水量“大于或等于4t且小于7t”为中等用水量家庭,请你估计总体小王所居住的小区中等用水量家庭大约有多少户?
(3)从月均用水量在2≤x<3,8≤x<9这两个范围内的样本家庭中任意抽取2个,请用列举法(画树状图或列表)求抽取出的2个家庭来自不同范围的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
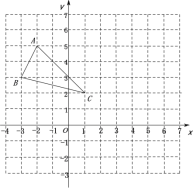
【题目】如图,在平面直角坐标系中,已知点A(-2,5),B(-3,3),C(1,2),点P(m,n)是三角形ABC内任意一点,三角形经过平移后得到三角形A1B1C1,点P的对应点为P1(m+6,n-2).
(1)直接写出平移后点A1、B1、C1的坐标分别为 .
(2)画出三角形ABC平移后的三角形A1B1C1..
查看答案和解析>>
科目:初中数学 来源: 题型:
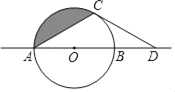
【题目】如图,⊙O半径为1,AB是⊙O的直径,C是⊙O上一点,连接AC,⊙O外的一点D 在直线AB上.
(1)若AC=![]() ,OB=BD.
,OB=BD.
①求证:CD是⊙O的切线.
②阴影部分的面积是 .(结果保留π)
(2)当点C在⊙O上运动时,若CD是⊙O的切线,探究∠CDO与∠OAC的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
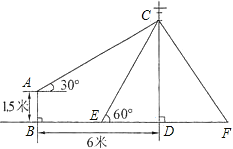
【题目】如图,在电线杆上的C处引拉线CE、CF固定电线杆,拉线CE和地面成60°角,在离电线杆6米的B处安置测角仪,在A处测得电线杆上C处的仰角为30°,已知测角仪高AB为1.5米,求拉线CE的长(结果保留根号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com