
����Ŀ����ͼ(1)��AB��CD�������BPD���B.��D�Ĺ�ϵ��˵�����ɣ�(��ʾ�������ε��ڽǺ͵���180��)
����ջ���д����
�⣺�����BPD+��B+��D=360��
���ɣ�����P��EF��AB��
���B+��BPE=180��______
��AB��CD��EF��AB��
��______��_____��(�������ֱ�߶��͵�����ֱ��ƽ�У���ô������ֱ��Ҳ����ƽ��)
���EPD+______=180��
���B+��BPE+��EPD+��D=360��
���B+��BPD+��D=360��
����������Ľ��ⷽ�����۲�ͼ(2)����֪AB��CD������ͼ�еġ�BPD���B.��D�Ĺ�ϵ����˵�����ɣ�
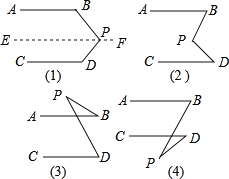
�۹۲�ͼ(3)��(4)����֪AB��CD��ֱ��д��ͼ�еġ�BPD���B.��D�Ĺ�ϵ����˵�����ɣ�
���𰸡���
��ֱ��ƽ�У�ͬ���ڽǻ�����CD��EF����CDP�ڲ����BPD����B����D�����ɼ������ۣ�3����BPD����B����D����4����BPD����B��D.
��������
�ٹ���P��EF��AB��������ֱ��ƽ�У�ͬ���ڽǻ�����֤�����ۣ�
����ٵķ������ƣ�����P��EP��AB��������ֱ��ƽ�У��ڴ�����ȣ�֤�����ۣ�
�۸���ƽ���ߵ����ʼ���������Ƕ���������⣮
�ٲ����BPD����B����D��360��
���ɣ�����P��EF��AB��
���B����BPE��180�㣨��ֱ��ƽ�У�ͬ���ڽǻ�����
��AB��CD��EF��AB��
��CD��EF�����������ֱ�߶��͵�����ֱ��ƽ�У���ô������ֱ��Ҳ����ƽ�У�
���EPD����CDP��180��
���B����BPE����EPD����D��360��
���B����BPD����D��360��
�����ֱ��ƽ�У�ͬ���ڽǻ�����CD��EF����CDP
�ڲ����BPD����B����D
���ɣ�����P��EP��AB��
���B����BPE����ֱ��ƽ�У�ͬλ����ȣ�
��AB��CD��EF��AB��
��CD��EF�����������ֱ�߶��͵�����ֱ��ƽ�У���ô������ֱ��Ҳ����ƽ�У�
���EPD����D
���BPD����B����D

����ͼ��3����PD��AB����O�㣬
��AB��CD�����D=��AOP��
�ߡ�AOP=��BPD����B��
���BPD����B����D��
����BPD����B����D�Ĺ�ϵΪ��BPD����B����D��
��ͼ��4����PB��CD����O�㣬
��AB��CD�����B=��COP��
�ߡ�COP=��BPD����D��
���BPD����D����B��
����BPD����B����D�Ĺ�ϵΪ��BPD����B��D.




| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����գ�С���Ӽ�����һ����ֱ�Ĺ�·����ȥ��ͤ����������һ��ʱ�������ԭ·���ؼ��У�С����ҵľ���y(��λ��m)�������õ�ʱ��t(��λ��min)֮��ĺ�����ϵ��ͼ��ʾ������˵���в���ȷ����( )
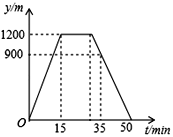
A. С�����뱨ͤ�ľ�����1200m
B. С���Ӽ�ȥ��ͤ��ƽ���ٶ���80m/min
C. С���ӱ�ͤ���ؼ��е�ƽ���ٶ���80m/min
D. С���ڱ�ͤ��������15min
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��![]() ��˫����
��˫����![]() �ཻ�ڵ�A(m��3)����x�ύ�ڵ�C.
�ཻ�ڵ�A(m��3)����x�ύ�ڵ�C.
(1)��˫���ߵĽ���ʽ��
(2)��P��x���ϣ������ACP�����Ϊ3�����P������.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������
��1������3.14��+��+4.96��+��+2.14��+����7.96��
��2����14������3��2��|��![]() |
|
��3������5��������3![]() ��+����7����3
��+����7����3![]() ��12������3
��12������3![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ʮһ���ƽ����ڼ䣬����������7�������ÿ���ο͵������仯���±���(������ʾ��ǰһ����������������ʾ��ǰһ���ٵ�����)

(1)��9��30�յ��ο�������Ϊa���ˣ����ú�a�Ĵ���ʽ��ʾ10��2�յ��ο�������
(2)���ж�7�����ο��������������죿
(3)��9��30�յ��ο�����Ϊ2���ˣ���Ʊÿ��10Ԫ���ʻƽ����ڼ�����������Ʊ�����Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���ABCD�У���ADC����ABC��90����AD��CD��DP��AB��P�����ı���ABCD�������18����DP�ij���________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
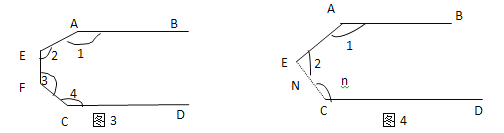
����Ŀ����֪����ͼ��AB��CD.
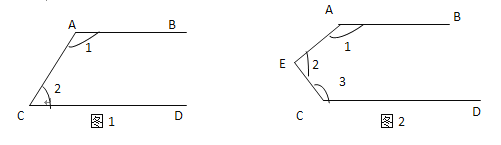
(1)��ͼ���еġ�1+��2�Ķ�����180��.
(2)��ͼ���еġ�1+��2+��3�Ķ����Ƕ���?
�⣺��ͼ�ݣ�����E��EF��AB(Ϊ�˽������Ҫ,���ӵ��߽��������ߣ������߳�����������).
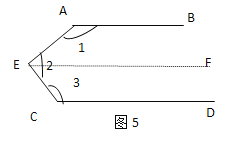
���ԡ�1+��AEF=180��.
��ΪAB��CD��
����CD��EF.
���ԡ�FEC+��3=180��.
���ԡ�1+��2+��3=360��.
�����Ķ�(2)�Ľ������,��ͼ���С�1+��2+��3+��4�Ķ����Ƕ���?̽��ͼ���С�1+��2+��3+��4+��+��n�Ķ����Ƕ���?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��y=x2+��1��a��x+1�ǹ���x�Ķ��κ�������x��ȡֵ��Χ��1��x��3ʱ��y��x=1ʱȡ�����ֵ����ʵ��a��ȡֵ��Χ�ǣ�������
A. a�ܩ�5 B. a��5 C. a=3 D. a��3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
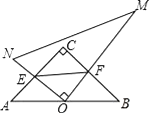
����Ŀ����Rt��ACB�У���C=90�㣬AC=BC��һֱ�����ǰ��ֱ�Ƕ���O��AB�ߵ��е��ϣ�������ǰ���O����ת������ֱ�DZ�ʼ����AC��BC�߷ֱ��ཻ��E��F������EF�������˶������У���OEF����ABC�Ĺ�ϵ�ǣ�������
A. һ������ B. ��E��AC�е�ʱ����
C. ��һ������ D. ���ж�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com