
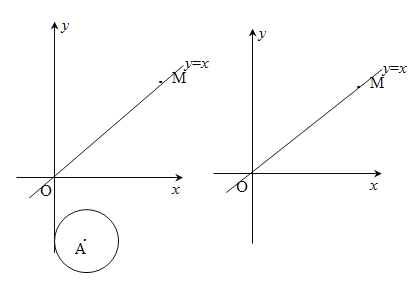
【题目】如图,在平面直角坐标系中,⊙A的半径为1,圆心A点的坐标为(1,﹣2).直线OM是一次函数y=x的图像.让⊙A沿y轴正方向以每秒1个单位长度移动,移动时间为t.
(1)填空:
①直线OM与x轴所夹的锐角度数为 °;
②当t= 时,⊙A与坐标轴有两个公共点;
(2)求出运动过程中⊙A与直线OM相切时的t的值.
【答案】(1)①45;②1秒或2秒或3秒;(2)![]() 或
或![]() .
.
【解析】
(1)①利用直线y=x上点的坐标特征易得直线y=x为第一、三象限的角平分线,则直线OM与x轴所夹的锐角度数为45°;
②根据直线与圆的位置关系得到⊙A沿y轴正方向运动时,⊙A始终与y轴相切,所以当⊙A与x轴相切或点A在x轴上时,⊙A与坐标轴有两个公共点,易得t=1或t=2或t=3;
(2)分两种情况画出图形,解答即可.
(1)①∵直线y=x上点到x轴和y轴的距离相等,∴直线y=x为第一、三象限的角平分线,∴直线OM与x轴所夹的锐角度数为45°;
②∵⊙A的半径为1,圆心A点的坐标为(1,﹣2),∴⊙A沿y轴正方向运动时,⊙A始终与y轴相切,当⊙A与x轴相切或点A在x轴上时,⊙A与坐标轴有两个公共点.
当⊙A与x轴相切时,则点A与x轴的距离为1,得到t=1或3;
当点A在x轴上,则t=2;
所以t=1或t=2或t=3.
故答案为:45,1秒或2秒或3秒;
(2)分两种情况讨论:
①如图1,作AB⊥y轴于B,AC⊥直线OM于C,AH⊥x轴于H,交直线OM于P,则OB=t﹣2,AB=AC=1,OH=1.
∵直线OM与x轴所夹的锐角度数为45°,∴∠POH=45°,∴∠OPH=45°,∴∠APC=45°,∴△OPH和△APC都是等腰直角三角形,∴PH=OH=1,AP![]() AC
AC![]() ,∴AH=AP+PH
,∴AH=AP+PH![]() 1,而AH=OB,∴t﹣2
1,而AH=OB,∴t﹣2![]() ,∴t=
,∴t=![]() ;
;
②如图2,作AB⊥y轴于B,AC⊥直线OM于C,CD⊥x轴于D,CD交BA与F,则OB=DF=2﹣t,AB=AC=1.
∵OB、OC都是⊙A的切线,∴OB=OC=2﹣t.
∵直线OM与x轴所夹的锐角度数为45°,∴∠COD=45°,∴△ODC是等腰直角三角形,∠OCD=45°,∴OD=CD=![]() =
=![]() .
.
∵∠OCA=90°,∠OCD=45°,∴∠ACF=45°,∴△ACF是等腰直角三角形,∴AC![]() AF.
AF.
∵AF=BA-BF=![]() ,∴
,∴![]() =1,解得:∴2﹣t=
=1,解得:∴2﹣t=![]() ,∴t=
,∴t=![]() .
.
综上所述:![]() 或
或![]() .
.



科目:初中数学 来源: 题型:
【题目】如图,![]() 个边长为
个边长为![]() 的相邻正方形的一边均在同一直线上,点
的相邻正方形的一边均在同一直线上,点![]() ,
,![]() ,
,![]() ,…
,…![]() 分别为边
分别为边![]() ,
,![]() ,
,![]() ,…,
,…,![]() 的中点,
的中点,![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,…
,…![]() 的面积为
的面积为![]() ,则
,则![]() ________.(用含
________.(用含![]() 的式子表示)
的式子表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E、F分别是边AB、CD上的点,AE=CF,连接EF,BF,EF与对角线AC交于O点,且BE=BF,∠BEF=2∠BAC。

(1)求证:OE=OF;
(2)若BC=![]() ,求AB的长。
,求AB的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2-4x-3,下列说法中正确的是( )
A.该函数图象的开口向下B.该函数图象的顶点坐标是(-2,-7)
C.当x<0时,y随x的增大而增大D.该函数图象与x轴有两个不同的交点,且分布在坐标原点两侧
查看答案和解析>>
科目:初中数学 来源: 题型:
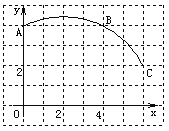
【题目】如图,在正方形网格图中建立一直角坐标系,一条圆弧经过网格点A、B、C,请回答:
(1)该圆弧所在圆心D点的坐标为 ;
(2)扇形DAC的圆心角度数为 ;
(3)若扇形DAC是某一个圆锥的侧面展开图,求该圆锥的高.(保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=(x+m)2+k的图象,其顶点坐标为M(1,﹣4).
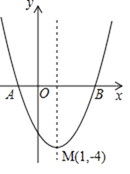
(1)求出图象与x轴的交点A、B的坐标;
(2)在y轴上存在一点Q,使得△QMB周长最小,求出Q点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解方程
(1)x2-7x+6=0
(2)(5x-1)2=3(5x-1)
(3) x2-4x-3=0 (用配方法)
(4) x2+4x+2=0(用公式法)
查看答案和解析>>
科目:初中数学 来源: 题型:
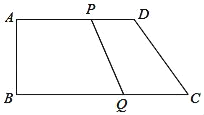
【题目】如图,在在四边形ABCD中,AD∥BC,∠B=90°,且AD=12cm,AB=8cm,DC=10cm,若动点P从A点出发,以每秒2cm的速度沿线段AD向点D运动;动点Q从C点出发以每秒3cm的速度沿CB向B点运动,当P点到达D点时,动点P、Q同时停止运动,设点P、Q同时出发,并运动了t秒,回答下列问题:
(1)BC= cm;
(2)当t= 秒时,四边形PQBA成为矩形.
(3)是否存在t,使得△DQC是等腰三角形?若存在,请求出t的值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某旅游景点的年游客量y(万人)是门票价格x(元)的一次函数,其函数图像如下图.

(1)求y关于x的函数解析式;
(2)经过景点工作人员统计发现:每卖出一张门票所需成本为20元.那么要想获得年利润11500万元,且门票价格不得高于230元,该年的门票价格应该定为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com