
【题目】如图,在平面直角坐标系中,A(1,2),B(3,1),C(-2,-1).
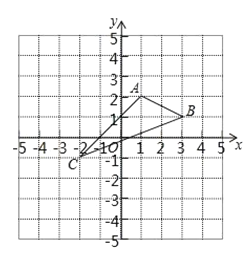
(1)作出△ABC关于y轴对称的△A1B1C1.
(2)△A1B1C1的面积为
(3)在y轴上作出点Q,使△QAB的周长最小.
 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,BD=CE,将线段AE沿AC翻折,得到线段AM,连结EM交AC于点N,连结DM、CM以下说法:①AD=AM,②∠MCA=60°,③CM=2CN,④MA=DM中,正确的有( )

A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,AB是⊙O的一条弦,OD⊥AB,垂足为C,交⊙O于点D,点E在⊙O上.
(1)若∠AOD=52°,求∠DEB的度数;
(2)若OC=3,OA=5,求AB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
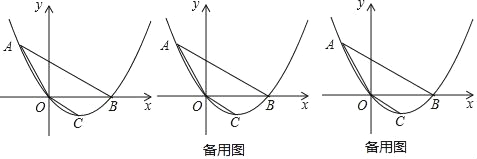
【题目】如图,顶点为C的抛物线y=ax2+bx(a>0)经过点A和x轴正半轴上的点B,连接OC、OA、AB,已知OA=OB=2,∠AOB=120°.
(1)求这条抛物线的表达式;
(2)过点C作CE⊥OB,垂足为E,点P为y轴上的动点,若以O、C、P为顶点的三角形与△AOE相似,求点P的坐标;
(3)若将(2)的线段OE绕点O逆时针旋转得到OE′,旋转角为α(0°<α<120°),连接E′A、E′B,求E′A+![]() E′B的最小值.
E′B的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边三角形![]() 的边长为4,点
的边长为4,点![]() 是△
是△![]() 的中心,
的中心,![]() .绕点
.绕点![]() 旋转
旋转![]() ,分别交线段
,分别交线段![]() 于
于![]() 两点,连接
两点,连接![]() ,给出下列四个结论:①
,给出下列四个结论:①![]() ;②
;②![]() ;③四边形
;③四边形![]() 的面积始终等于
的面积始终等于![]() ;④△
;④△![]() 周长的最小值为6,上述结论中正确的个数是( )
周长的最小值为6,上述结论中正确的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程(组)解应用题:
为顺利通过国家义务教育均衡发展验收,我市某中学配备了两个多媒体教室,购买了笔记本电脑和台式电脑共120台,购买笔记本电脑用了7.2万元,购买台式电脑用了24万元,已知笔记本电脑单价是台式电脑单价的1.5倍,那么笔记本电脑和台式电脑的单价各是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
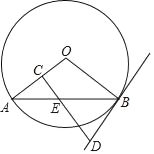
【题目】如图,AB是⊙O的一条弦,E是AB的中点,过点E作EC⊥OA于点C,过点B作⊙O的切线交CE的延长线于点D.
(1)求证:DB=DE;
(2)若AB=12,BD=5,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,点![]() 是正比例函数
是正比例函数![]() 与反比例函数
与反比例函数![]() 的图象在第一象限的交点,
的图象在第一象限的交点,![]() 轴,垂足为点
轴,垂足为点![]() ,
,![]() 的面积是2.
的面积是2.

(1)求![]() 的值以及这两个函数的解析式;
的值以及这两个函数的解析式;
(2)若点![]() 在
在![]() 轴上,且
轴上,且![]() 是以
是以![]() 为腰的等腰三角形,求点
为腰的等腰三角形,求点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com