
分析 (1)抛物线与x轴只有一个公共点,则判别式△=0,据此即可求得k的值;
(2)把C1化成顶点式的形式,利用函数平移的法则即可确定;
(3)首先求得t的值,然后求得等y=t时C2中对应的自变量的值,结合函数的性质即可求解.
解答 解:(1)根据题意得:△=16-8k=0,解得:k=2;
(2)C1是:y1=2x2-4x+2=2(x-1)2,抛物线C2是:y2=2(x+1)2-8.
则平移抛物线C1就可以得到抛物线C2的方法是向左平移2个单位长度,向下平移8个单位长度;
(3)当x=1时,y2=2(x+1)2-8=0,即t=0.
在y2=2(x+1)2-8中,令y=0,解得:x=1或-3.
则当n<t时,即2(x+1)2-8<0时,m的范围是-3<m<1.
点评 本题考查抛物线与x轴的交点的个数的确定,以及函数的平移方法,根据函数的性质确定m的范围是关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
 某校要举办国庆联欢会,主持人站在舞台的黄金分割点处最自然得体.如图,若舞台AB的长为20m,C为AB的一个黄金分割点(AC<BC),则AC的长为(结果精确到0.1m)( )
某校要举办国庆联欢会,主持人站在舞台的黄金分割点处最自然得体.如图,若舞台AB的长为20m,C为AB的一个黄金分割点(AC<BC),则AC的长为(结果精确到0.1m)( )| A. | 6.7m | B. | 7.6m | C. | 10m | D. | 12.4m |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
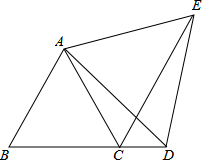 如图,已知△ABC为等边三角形,D为BC延长线上的一点,CE平分∠ACD,
如图,已知△ABC为等边三角形,D为BC延长线上的一点,CE平分∠ACD,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
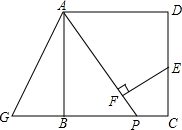 如图,P为正方形ABCD边BC上一点,F在AP上,AF=AD,EF⊥AP于F交CD于点E,G为CB延长线上一点,且BG=DE.
如图,P为正方形ABCD边BC上一点,F在AP上,AF=AD,EF⊥AP于F交CD于点E,G为CB延长线上一点,且BG=DE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com