
分析 (1)根据题意可以分表示出该商店前20天的日销售利润R1(元)和后10天的日销售利润R2(元)与销售时间x(天)之间的函数关系式;
(2)有第一问中的函数关系式可以分别求出在各自范围内的最大值,然后进行比较即可解答本题.
解答 解:(1)由题意可得,
R1=P(Q1-20)=(-2x+80)[($\frac{1}{2}$x+30)-20]=-x2+20x+800,
R2=P(Q2-20)=(-2x+80)(45-20)=-50x+2000,
即该商店前20天的日销售利润R1(元)和后10天的日销售利润R2(元)与销售时间x(天)之间的函数关系式分别是:${R}_{1}=-{x}^{2}+20x+800,{R}_{2}=-50x+2000$;
(2)∵当1≤x≤20时,R1=-(x-10)2+900,
∴当x=10时,R1的最大值为900,
当21≤x≤30时,R2=-50x+2000,
∵R2的值随x值的增大而减小,∴当x=21时,R2的最大值是950,
∵950>900,
∴在第21天时,日销售利润最大,最大利润为950元.
点评 本题考查二次函数的应用,解题的关键是明确题意可以列出相应的函数关系式,并可以求函数的最值.


科目:初中数学 来源: 题型:解答题
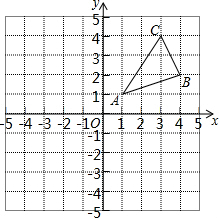 如图,△ABC三个顶点的坐标分别为A(1,1)、B(4,2)、C(3,4).
如图,△ABC三个顶点的坐标分别为A(1,1)、B(4,2)、C(3,4).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知抛物线的顶点为(0,4)且与x轴交于(-2,0),(2,0).
已知抛物线的顶点为(0,4)且与x轴交于(-2,0),(2,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com