
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 分别是边
分别是边![]() 上的动点(点
上的动点(点![]() 不与
不与![]() 重合),且
重合),且![]() ,过点
,过点![]() 作
作![]() 的平行线
的平行线![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,设
,设![]() 为
为![]() .
.
(1)试说明不论![]() 为何值时,总有
为何值时,总有![]() ∽
∽![]() ;
;
(2)是否存在一点![]() ,使得四边形
,使得四边形![]() 为平行四边形,试说明理由;
为平行四边形,试说明理由;
(3)当![]() 为何值时,四边形
为何值时,四边形![]() 的面积最大,并求出最大值.
的面积最大,并求出最大值.

 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两个工程队需完成A、B两个工地的工程.若甲、乙两个工程队分别可提供40个和50个标准工作量,完成A、B两个工地的工程分别需要70个和20个标准工作量,且两个工程队在A、B两个工地的1个标准工作量的成本如下表所示:
A工地 | B工地 | |
甲工程队 | 800元 | 750元 |
乙工程队 | 600元 | 570元 |
设甲工程队在A工地投入x(20≤x≤40)个标准工作量,完成这两个工程共需成本y元.
(1)求y与x之间的函数关系式;
(2)请判断y是否能等于62000,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
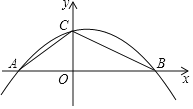
【题目】如图,在直角坐标系中,直线![]() 与
与![]() 轴,
轴,![]() 轴分别交于点
轴分别交于点![]() ,点
,点![]() ,对称轴为
,对称轴为![]() 的抛物线过
的抛物线过![]() 两点,且交
两点,且交![]() 轴于另一点
轴于另一点![]() ,连接
,连接![]() .
.
(1)直接写出点![]() ,点
,点![]() ,点
,点![]() 的坐标和抛物线的解析式;
的坐标和抛物线的解析式;
(2)已知点![]() 为第一象限内抛物线上一点,当点
为第一象限内抛物线上一点,当点![]() 到直线
到直线![]() 的距离最大时,求点
的距离最大时,求点![]() 的坐标;
的坐标;
(3)抛物线上是否存在一点![]() (点
(点![]() 除外),使以点
除外),使以点![]() ,
,![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 相似?若存在,求出点
相似?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某村2016年的人均收入为20000元,2018年的人均收入为24200元
(1)求2016年到2018年该村人均收入的年平均增长率;
(2)假设2019年该村人均收入的增长率与前两年的年平均增长率相同,请你预测2019年村该村的人均收入是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两条抛物线![]() 与
与![]() 的顶点相同.
的顶点相同.
(1)求抛物线![]() 的解析式;
的解析式;
(2)点![]() 是抛物找
是抛物找![]() 在第四象限内图象上的一动点,过点
在第四象限内图象上的一动点,过点![]() 作
作![]() 轴,
轴,![]() 为垂足,求
为垂足,求![]() 的最大值;
的最大值;
(3)设抛物线![]() 的顶点为点
的顶点为点![]() ,点
,点![]() 的坐标为
的坐标为![]() ,问在
,问在![]() 的对称轴上是否存在点
的对称轴上是否存在点![]() ,使线段
,使线段![]() 绕点
绕点![]() 顺时针旋转90°得到线段
顺时针旋转90°得到线段![]() ,且点
,且点![]() 恰好落在抛物线
恰好落在抛物线![]() 上?若存在,求出点
上?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了进一步丰富校园活动,学校准备购买一批足球和篮球,已知购买7个足球和5个篮球的费用相同;购买40个足球和20个篮球共需3400元.
(1)求每个足球和篮球各多少元?
(2)如果学校计划购买足球和篮球共80个,总费用不超过4800元,那么最多能买多少个篮球?
查看答案和解析>>
科目:初中数学 来源: 题型:
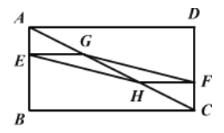
【题目】如图,在矩形ABCD中,AB=3,BC=6,若点E,F分别在AB,CD上,且BE=2AE,DF=2FC,G,H分别是AC的三等分点,则四边形EHFG的面积为( )
A. 1B. ![]() C. 2D. 4
C. 2D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() (
(![]() 为常数,
为常数,![]() ),其对称轴是
),其对称轴是![]() ,与
,与![]() 轴的一个交点在
轴的一个交点在![]() ,
,![]() 之间.有下列结论:①
之间.有下列结论:①![]() ;②
;②![]() ;③若此抛物线过
;③若此抛物线过![]() 和
和![]() 两点,则
两点,则![]() ,其中,正确结论的个数为( )
,其中,正确结论的个数为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
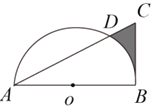
【题目】如图,在Rt△ABC中,∠ABC=90°,AB=![]() ,BC=2,以AB的中点为圆心,OA的长为半径作半圆交AC于点D,则图中阴影部分的面积为( )
,BC=2,以AB的中点为圆心,OA的长为半径作半圆交AC于点D,则图中阴影部分的面积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com