
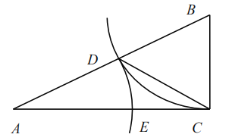
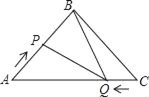
【题目】如图,在△ABC中,∠ACB=90°,以点B为圆心,BC长为半径画弧,交边AB与点D,以A为圆心,AD长为半径画弧,交边AC于点E,连接CD.
(1)若∠A=28°,求∠ACD的度数;
(2)设BC=a,AC=b.
①线段AD的长是方程![]() 的一个根吗?为什么?
的一个根吗?为什么?
②若AD=EC,求![]() 的值.
的值.
【答案】(1)31°;(2)①是,理由见解析;②![]() .
.
【解析】
(1)根据三角形内角和定理求出∠B,根据等腰三角形的性质求出∠BCD,计算即可;
(2)①根据勾股定理求出AD,利用求根公式解方程,比较即可;
②根据勾股定理列出算式,计算即可.
(1)∵∠ACB=90°,∠A=28°,
∴∠B=62°,
∵BD=BC,
∴∠BCD=∠BDC=59°,
∴∠ACD=90°-∠BCD=31°;
(2)①由勾股定理得,AB=![]() ,
,
∴AD=![]() -a,
-a,
解方程x2+2ax-b2=0得,x=![]() =±
=±![]() -a,
-a,
∴线段AD的长是方程x2+2ax-b2=0的一个根;
②∵AD=AE,
∴AE=EC=![]() ,
,
由勾股定理得,a2+b2=(![]() b+a)2,
b+a)2,
整理得,![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,AD是圆O的切线,切点为A,AB是圆O的弦。过点B作BC//AD,交圆O于点C,连接AC,过点C作CD//AB,交AD于点D。连接AO并延长交BC于点M,交过点C的直线于点P,且BCP=ACD。
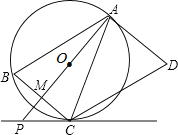
(1)判断直线PC与圆O的位置关系,并说明理由:
(2) 若AB=9,BC=6,求PC的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
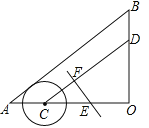
【题目】如图,△AOB中,∠O=90°,AO=8cm,BO=6cm,点C从A点出发,在边AO上以2cm/s的速度向O点运动,与此同时,点D从点B出发,在边BO上以1.5cm/s的速度向O点运动,过OC的中点E作CD的垂线EF,则当点C运动了__s时,以C点为圆心,1.5cm为半径的圆与直线EF相切.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场一种商品的进价为每件30元,售价为每件40元.每天可以销售48件,为尽快减少库存,商场决定降价促销.
(1)若该商品连续两次下调相同的百分率后售价降至每件32.4元,求两次下降的百分率;
(2)经调查,若每降价0.5元,每天可多销售4件,那么每天要想获得510元的利润,每件应降价多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图 1,在△ABC 中,∠ACB=90°,BC=AC,点 D 在 AB 上,DE⊥AB交 BC 于 E,点 F 是 AE 的中点
(1) 写出线段 FD 与线段 FC 的关系并证明;
(2) 如图 2,将△BDE 绕点 B 逆时针旋转α(0°<α<90°),其它条件不变,线段 FD 与线段 FC 的关系是否变化,写出你的结论并证明;
(3) 将△BDE 绕点 B 逆时针旋转一周,如果 BC=4,BE=2![]() ,直接写出线段 BF 的范围.
,直接写出线段 BF 的范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
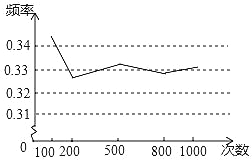
【题目】某学习小组做“用频率估计概率的试验时,统计了某一结果出现的频率,绘制了如图所示折线统计图,则符合这一结果的试验最有可能的是( )
A. 掷一枚正六面体的骰子,出现1点朝上
B. 任意写一个整数,它能被2整除
C. 不透明袋中装有大小和质地都相同的1个红球和2个黄球,从中随机取一个,取到红球
D. 先后两次掷一枚质地均匀的硬币,两次都出现反面
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 从
从![]() 点出发,沿着
点出发,沿着![]() 以每秒
以每秒![]() 的速度向
的速度向![]() 点运动;同时点
点运动;同时点![]() 从
从![]() 点出发,沿
点出发,沿![]() 以每秒
以每秒![]() 的速度向
的速度向![]() 点运动,设运动时间为
点运动,设运动时间为![]() 秒.
秒.
(1)当![]() 为何值时,
为何值时,![]() ;
;
(2)是否存在某一时刻,使![]() ?若存在,求出此时
?若存在,求出此时![]() 的长;若不存在,请说理由;
的长;若不存在,请说理由;
(3)当![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校初三体育考试选择项目中,选择篮球项目和排球项目的学生比较多.为了解学生掌握篮球技巧和排球技巧的水平情况,进行了抽样调查,过程如下,请补充完整.
收集数据 从选择篮球和排球的学生中各随机抽取16人,进行了体育测试,测试成绩(十分制)如下:
排球 10 9.5 9.5 10 8 9 9.5 9
7 10 4 5.5 10 9.5 9.5 10
篮球 9.5 9 8.5 8.5 10 9.5 10 8
6 9.5 10 9.5 9 8.5 9.5 6
整理、描述数据 按如下分数段整理、描述这两组样本数据:
4.0≤x<5.5 | 5.5≤x<7.0 | 7.0≤x<8.5 | 8.5≤x<10 | 10 | |
排球 | 1 | 1 | 2 | 7 | 5 |
篮球 |
(说明:成绩8.5分及以上为优秀,6分及以上为合格,6分以下为不合格.)
分析数据 两组样本数据的平均数、中位数、众数如下表所示:
项目 | 平均数 | 中位数 | 众数 |
排球 | 8.75 | 9.5 | 10 |
篮球 | 8.81 | 9.25 | 9.5 |
得出结论
(1)如果全校有160人选择
(2)初二年级的小明和小军看到上面数据后,小明说:排球项目整体水平较高.小军说:篮球项目整体水平较高.
你同意______ 的看法,理由为__________.(至少从两个不同的角度说明推断的合理性)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x函数y=(2﹣k)x2﹣2x+k
(1)若此函数的图象与坐标轴只有2个交点,求k的值.
(2)求证:关于x的一元二次方程(2﹣k)x2﹣2x+k=0必有一个根是1.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com