
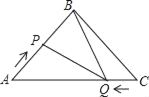
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 从
从![]() 点出发,沿着
点出发,沿着![]() 以每秒
以每秒![]() 的速度向
的速度向![]() 点运动;同时点
点运动;同时点![]() 从
从![]() 点出发,沿
点出发,沿![]() 以每秒
以每秒![]() 的速度向
的速度向![]() 点运动,设运动时间为
点运动,设运动时间为![]() 秒.
秒.
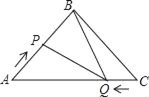
(1)当![]() 为何值时,
为何值时,![]() ;
;
(2)是否存在某一时刻,使![]() ?若存在,求出此时
?若存在,求出此时![]() 的长;若不存在,请说理由;
的长;若不存在,请说理由;
(3)当![]() 时,求
时,求![]() 的值.
的值.
【答案】(1)当x=![]() 时,PQ∥BC;(2)存在,AP=
时,PQ∥BC;(2)存在,AP=![]() ;(3)
;(3)![]() =
=![]() .
.
【解析】
(1)由PQ∥BC,得出比例式![]() ,即可求出x的值;
,即可求出x的值;
(2)由BA=BC得∠A=∠C.要使△APQ∽△CQB,只需![]() ,此时
,此时![]() 解这个方程就可解决问题.
解这个方程就可解决问题.
(3)当CQ=10时,可求出x,从而求出AP,即可求出BP,然后根据两个三角形两底上的高相等时,这两个三角形的面积比等于这两个底的比,就可解决问题;
解:(1)由题可得AP=4x,CQ=3x.
∵BA=BC=20,AC=30,
∴BP=20﹣4x,AQ=30﹣3x.
若PQ∥BC,
则有△APQ∽△ABC,
∴![]()
∴![]()
解得:x=![]() .
.
∴当x=![]() 时,PQ∥BC;
时,PQ∥BC;
(2)存在.
∵BA=BC,∴∠A=∠C.
要使△APQ∽△CQB,
只需![]()
此时![]()
解得:x=![]() ,
,
∴AP=4x=![]() ;
;
(3)当CQ=10时,3x=10,
∴x=![]() ,
,
∴AP=4x=![]() ,
,
∴![]()


科目:初中数学 来源: 题型:
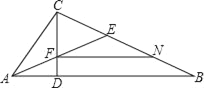
【题目】如图,在△ABC中,CD⊥AB,且CD2=ADDB,AE平分∠CAB交CD于F,∠EAB=∠B,CN=BE.①CF=BN;②∠ACB=90°;③FN∥AB;④AD2=DFDC.则下列结论正确的是( )
A. ①②④ B. ②③④ C. ①②③④ D. ①③
查看答案和解析>>
科目:初中数学 来源: 题型:
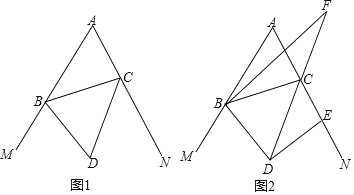
【题目】如图1,在△ABC中,∠A=60°,∠CBM,∠BCN是△ABC的外角,∠CBM,∠BCN的平分线BD,CD交于点D.
(1)求∠BDC的度数;
(2)在图1中,过点D作DE⊥BD,垂足为点D,过点B作BF∥DE交DC的延长线于点F(如图2),求证:BF是∠ABC的平分线.
查看答案和解析>>
科目:初中数学 来源: 题型:
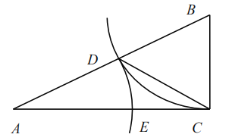
【题目】如图,在△ABC中,∠ACB=90°,以点B为圆心,BC长为半径画弧,交边AB与点D,以A为圆心,AD长为半径画弧,交边AC于点E,连接CD.
(1)若∠A=28°,求∠ACD的度数;
(2)设BC=a,AC=b.
①线段AD的长是方程![]() 的一个根吗?为什么?
的一个根吗?为什么?
②若AD=EC,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD和平行四边形BEFG中,已知AB=BC,BG=BE,点A,B,E在同一直线上,P是线段DF的中点,连接PG,PC,若∠DCB=∠GEF=120°,则![]() =( )
=( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《如果想毁掉一个孩子,就给他一部手机!》这是2017年微信圈一篇热传的文章.国际上,法国教育部宣布从 2018 年9月新学期起小学和初中禁止学生使用手机.为了解学生手机使用情况,某学校开展了“手机伴我健康行”主题活动,他们随机抽取部分学生进行“使用手机目的”和“每周使用手机的时间”的问卷调查,并绘制成如图①,②的 统计图,已知“查资料”的人数是 40人.请你根据以上信息解答下列问题:
(1)在扇形统计图中,“玩游戏”对应的百分比为______,圆心角度数是______度;
(2)补全条形统计图;
(3)该校共有学生2100人,估计每周使用手机时间在2 小时以上(不含2小时)的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=2,BC=4.将矩形ABCD绕点C沿顺时针方向旋转90°后,得到矩形FGCE(点A、B、D的对应点分别为点F、G、E).动点P从点B开始沿BC-CE运动到点E后停止,动点Q从点E开始沿EF-FG运动到点G后停止,这两点的运动速度均为每秒1个单位.若点P和点Q同时开始运动,运动时间为x(秒),△APQ的面积为y,则能够正确反映y与x之间的函数关系的图象大致是( )

A. 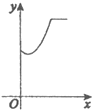 B.
B. 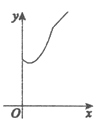 C.
C. 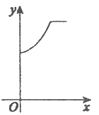 D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=6cm,BC=7cm,∠ABC=30°,点P从A点出发,以1cm/s的速度向B点移动,点Q从B点出发,以2cm/s的速度向C点移动.如果P、Q两点同时出发,经过几秒后△PBQ的面积等于4cm2?
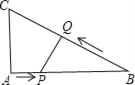
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, 抛物线![]() 与
与![]() 轴交于点A(-1,0),顶点坐标(1,n)与
轴交于点A(-1,0),顶点坐标(1,n)与![]() 轴的交点在(0,2),(0,3)之间(包 含端点),则下列结论:①
轴的交点在(0,2),(0,3)之间(包 含端点),则下列结论:①![]() ;②
;②![]() ;③对于任意实数m,
;③对于任意实数m,![]() 总成立;④关于
总成立;④关于![]() 的方程
的方程![]() 有两个不相等的实数根.其中结论正确的个数为
有两个不相等的实数根.其中结论正确的个数为![]()
![]()

A. 1 个 B. 2 个 C. 3 个 D. 4 个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com