
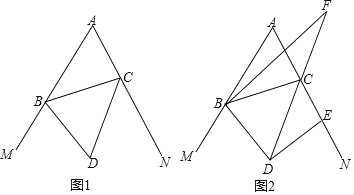
【题目】如图1,在△ABC中,∠A=60°,∠CBM,∠BCN是△ABC的外角,∠CBM,∠BCN的平分线BD,CD交于点D.
(1)求∠BDC的度数;
(2)在图1中,过点D作DE⊥BD,垂足为点D,过点B作BF∥DE交DC的延长线于点F(如图2),求证:BF是∠ABC的平分线.
【答案】(1)∠BDC=60°;(2)证明见解析.
【解析】
(1)依据三角形内角和定理可得,∠ABC+∠ACB=120°,进而得出∠CBM+∠BCN=360°﹣120°=240°,再根据∠CBM,∠BCN的平分线BD,CD交于点D,即可得到,∠DBC+∠BCD=120°,即可得出∠D=180°﹣120°=60°;
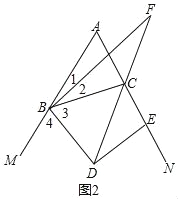
(2)依据DE⊥BD,BF∥DE,即可得出∠2+∠3=90°,∠1+∠4=90°,再根据∠3=∠4,可得∠1=∠2,进而得到BF是∠ABC的平分线.
解:(1)∵△ABC中,∠A=60°,
∴∠ABC+∠ACB=120°,
又∵∠ABM=∠ACN=180°,
∴∠CBM+∠BCN=360°﹣120°=240°,
又∵∠CBM,∠BCN的平分线BD,CD交于点D,
∴∠CBD=![]() ∠CBM,∠BCD=
∠CBM,∠BCD=![]() ∠BCN,
∠BCN,
∴△BCD中,∠DBC+∠BCD=![]() (∠CBM+∠BCN)=
(∠CBM+∠BCN)=![]() ×240°=120°,
×240°=120°,
∴∠D=180°﹣120°=60°;
(2)如图2,∵DE⊥BD,BF∥DE,
∴∠DBF=180°﹣90°=90°,
即∠2+∠3=90°,
∴∠1+∠4=90°,
又∵∠3=∠4,
∴∠1=∠2,
∴BF是∠ABC的平分线.


 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】A,B两地被大山阻隔,若要从A地到B地,只能沿着如图所示的公路先从A地到C地,再由C地到B地.现计划开凿隧道A,B两地直线贯通,经测量得:∠CAB=30°,∠CBA=45°,AC=20km,求隧道开通后与隧道开通前相比,从A地到B地的路程将缩短多少?(结果精确到0.1km,参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.732)
≈1.732)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次课题学习中活动中,老师提出了如下一个问题:
点P是正方形ABCD内的一点,过点P画直线l分别交正方形的两边于点M、N,使点P是线段MN的三等分点,这样的直线能够画几条?
经过思考,甲同学给出如下画法:
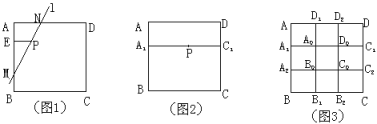
如图1,过点P画PE⊥AB于E,在EB上取点M,使EM=2EA,画直线MP交AD于N,则直线MN就是符合条件的直线l.
根据以上信息,解决下列问题:
(1)甲同学的画法是否正确?请说明理由.
(2)在图1中,能否画出符合题目条件的直线?如果能,请直接在图1中画出.
(3)如图2,A1、C1分别是正方形ABCD的边AB、CD上的三等分点,且A1C1∥AD.当点P在线段A1C1上时,能否画出符合题目条件的直线?如果能,可以画出几条?
(4)如图3,正方形ABCD边界上的A1、A2、B1、B2、C1、C2、D1、D2都是所在边的三等分点.当点P在正方形ABCD内的不同位置时,试讨论,符合题目条件的直线l的条数的情况.
查看答案和解析>>
科目:初中数学 来源: 题型:
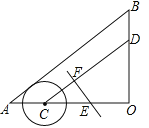
【题目】如图,△AOB中,∠O=90°,AO=8cm,BO=6cm,点C从A点出发,在边AO上以2cm/s的速度向O点运动,与此同时,点D从点B出发,在边BO上以1.5cm/s的速度向O点运动,过OC的中点E作CD的垂线EF,则当点C运动了__s时,以C点为圆心,1.5cm为半径的圆与直线EF相切.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对角线长分别为6和8的菱形ABCD如图所示,点O为对角线的交点,过点O折叠菱形,使B,B′两点重合,MN是折痕.若B'M=1,则CN的长为( )
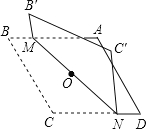
A. 7 B. 6 C. 5 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场一种商品的进价为每件30元,售价为每件40元.每天可以销售48件,为尽快减少库存,商场决定降价促销.
(1)若该商品连续两次下调相同的百分率后售价降至每件32.4元,求两次下降的百分率;
(2)经调查,若每降价0.5元,每天可多销售4件,那么每天要想获得510元的利润,每件应降价多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图 1,在△ABC 中,∠ACB=90°,BC=AC,点 D 在 AB 上,DE⊥AB交 BC 于 E,点 F 是 AE 的中点
(1) 写出线段 FD 与线段 FC 的关系并证明;
(2) 如图 2,将△BDE 绕点 B 逆时针旋转α(0°<α<90°),其它条件不变,线段 FD 与线段 FC 的关系是否变化,写出你的结论并证明;
(3) 将△BDE 绕点 B 逆时针旋转一周,如果 BC=4,BE=2![]() ,直接写出线段 BF 的范围.
,直接写出线段 BF 的范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 从
从![]() 点出发,沿着
点出发,沿着![]() 以每秒
以每秒![]() 的速度向
的速度向![]() 点运动;同时点
点运动;同时点![]() 从
从![]() 点出发,沿
点出发,沿![]() 以每秒
以每秒![]() 的速度向
的速度向![]() 点运动,设运动时间为
点运动,设运动时间为![]() 秒.
秒.
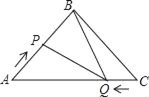
(1)当![]() 为何值时,
为何值时,![]() ;
;
(2)是否存在某一时刻,使![]() ?若存在,求出此时
?若存在,求出此时![]() 的长;若不存在,请说理由;
的长;若不存在,请说理由;
(3)当![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
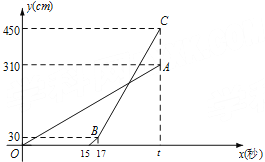
【题目】甲乙两台智能机器人从同一地点出发,沿着笔直的路线行走了450cm.甲比乙先出发,乙出发一段时间后速度提高为原来的2倍.两机器人行走的路程y(cm)与时间x(s)之间的函数图像如图所示,根据图像所提供的信息解答下列问题:
(1)乙比甲晚出发_________秒,乙提速前的速度是每秒_________cm, ![]() =_________;
=_________;
(2)已知甲匀速走完了全程,请补全甲的图象;
(3)当x为何值时,乙追上了甲?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com