
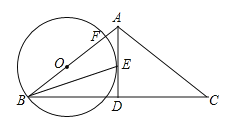
【题目】如图,在△ABC中,AB=AC,AD是角平分线,BE平分∠ABC交AD于点E,点O在AB上,以OB为半径的⊙O经过点E,交AB于点F.
(1)求证:AD是⊙O的切线;
(2)若AC=4,∠C=30°,求![]() 的长.
的长.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)连接OE,利用角平分线的定义和圆的性质可得∠OBE=∠OEB=∠EBD,可证明OE∥BD,结合等腰三角形的性质可得AD⊥BD,可证得OE⊥AD,可证得AD为切线;
(2)利用(1)的结论,结合条件可求得∠AOE=30°,由AC的长可求得圆的半径,利用弧长公式可求得![]() .
.
试题解析:(1)证明:如图,连接OE,∵OB=OE,∴∠OBE=∠OEB,∵BE平分∠ABC,∴∠OBE=∠EBD,∴∠OEB=∠EBD,∴OE∥BD,∵AB=AC,AD平分∠BAC,∴AD⊥BC,∴∠OEA=∠BDA=90°,∴AD是⊙O的切线;
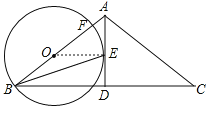
(2)解:∵AB=AC=4,∴OB=OE=OF=2,由(1)可知OE∥BC,且AB=AC,∴∠AOE=∠ABC=∠C=30°,∴![]() =
=![]() =
=![]() .
.


科目:初中数学 来源: 题型:
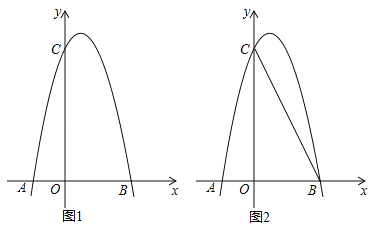
【题目】如图1,对称轴为直线x=![]() 的抛物线经过B(2,0)、C(0,4)两点,抛物线与x轴的另一交点为A.
的抛物线经过B(2,0)、C(0,4)两点,抛物线与x轴的另一交点为A.
(1)求抛物线的解析式;
(2)若点P为第一象限内抛物线上的一点,设四边形COBP的面积为S,求S的最大值;
(3)如图2,若M是线段BC上一动点,在x轴是否存在这样的点Q,使△MQC为等腰三角形且△MQB为直角三角形?若存在,求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把△ABC向上平移4个的那位长度,再向右平移3个单位长度,得到△A′B′C′.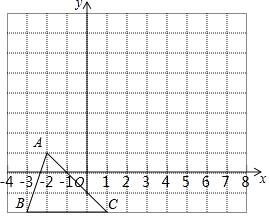
(1)在图中画出△A′B′C′;
(2)连接A′A、C′C,求四边形A′AC′C的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD的对角线交于点O,下列哪组条件不能判断四边形ABCD是平行四边形( )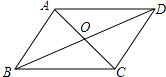
A.OA=OC,OB=OD
B.AB=CD,AO=CO
C.AD∥BC,AD=BC
D.∠BAD=∠BCD,AB∥CD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,∠C=90°,AC<BC,D为BC上一点,且到A、B两点的距离相等. 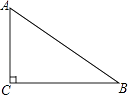
(1)用直尺和圆规,作出点D的位置(不写作法,保留作图痕迹);
(2)连结AD,若∠B=32°,求∠CAD的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com