
【题目】小聪与同桌小明在课下学习中遇到这样一道数学题:“如图(1),在等边三角形ABC中,点E在AB上,点D在CB的延长线上,且ED=EC,试确定线段AE与DB的大小关系,并说明理由”.小敏与小颖讨论后,进行了如下解答: 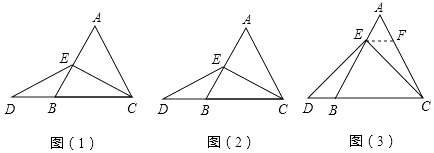
(1)取特殊情况,探索讨论: 当点E为AB的中点时,如图(2),确定线段AE与DB的大小关系,请你写出结论:AEDB(填“>”,“<”或“=”),并说明理由.
(2)特例启发,解答题目: 解:题目中,AE与DB的大小关系是:AEDB(填“>”,“<”或“=”).理由如下:如图(3),过点E作EF∥BC,交AC于点F.(请你将剩余的解答过程完成)
(3)拓展结论,设计新题: 在等边三角形ABC中,点E在直线AB上,点D在直线BC上,且ED=EC,若△ABC的边长为1,AE=2,则CD的长为 . (请你画出图形,并直接写出结果).
【答案】
(1)=
(2)=
(3)3或1
【解析】解:(1.)AE=DB, 理由如下:∵ED=EC,
∴∠EDC=∠ECD,
∵三角形ABC是等边三角形,
∴∠ACB=∠ABC=60°,
∵点E为AB的中点,
∴∠ECD= ![]() ∠ACB=30°,
∠ACB=30°,
∴∠EDC=30°,
∴∠D=∠DEB=30°,
∴DB=BE,
∵AE=BE,
∴AE=DB,
所以答案是:=;
(2.)如图3,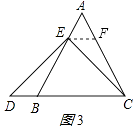
∵△ABC为等边三角形,且EF∥BC,
∴∠AEF=∠ABC=60°,∠AFE=∠ACB=60°,∠FEC=∠ECB,
∴∠EFC=∠DBE=120°,
∵ED=EC,
∴∠D=∠ECB,∠D=∠FEC,
在△EFC与△DBE中,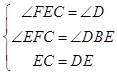 ,
,
∴△EFC≌△DBE(AAS),
∴EF=DB,
∵∠AEF=∠AFE=60°,
∴△AEF为等边三角形,
∴AE=EF,AE=BD,
所以答案是:=;
(3.)如图4,当点E在AB的延长线上时,过点E作EF∥BC,交AC的延长线于点F,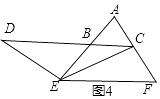
则∠DCE=∠CEF,∠DBE=∠AEF,∠ABC=∠AEF,∠ACB=∠AFE,
∵△ACB为等边三角形,
∴∠ABC=∠ACB=60°,
∴∠AEF=∠AFE=60°,∠DBE=∠ABC=60°,
∴∠DBE=∠EFC,而ED=EC,
∴∠D=∠DCE,∠D=∠CEF,
在△BDE与△FEC中,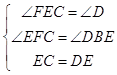 ,
,
∴△BDE≌△FEC(AAS),
∴BD=EF,
∵△AEF为等边三角形,
∴AE=EF=2,BD=EF=2,
∴CD=1+2=3;
如图5,当点E在BA的延长线上时,过点E作EF∥BC,交CA的延长线于点F,
类似上述解法,同理可证:DB=EF=2,BC=1,
∴CD=2﹣1=1,
所以答案是:3或1.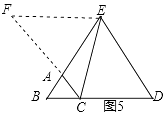


科目:初中数学 来源: 题型:
【题目】某校在践行“社会主义核心价值观”演讲比赛中,对名列前20名的选手的综合分数m进行分组统计,结果如表所示:

(1)求a的值;
(2)若用扇形图来描述,求分数在8≤m<9内所对应的扇形图的圆心角大小;
(3)将在第一组内的两名选手记为:A1、A2,在第四组内的两名选手记为:B1、B2,从第一组和第四组中随机选取2名选手进行调研座谈,求第一组至少有1名选手被选中的概率(用树状图或列表法列出所有可能结果).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C在一次函数y=﹣2x+m的图象上,它们的横坐标依次为﹣1,1,2,分别过这些点作x轴与y轴的垂线,则图中阴影部分的面积之和是( )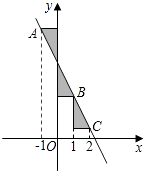
A.1
B.3
C.3(m﹣1)
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的平面直角坐标系中,△OA1B1是边长为2的等边三角形,作△B2A2B1与△OA1B1关于点B1成中心对称,再作△B2A3B3与△B2A2B1关于点B2成中心对称,如此作下去,则△B2nA2n+1B2n+1(n是正整数)的顶点A2n+1的坐标是( )

A.(4n﹣1,![]() ) B.(2n﹣1,
) B.(2n﹣1,![]() ) C.(4n+1,
) C.(4n+1,![]() ) D.(2n+1,
) D.(2n+1,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com