
【题目】如图,在 ![]() 中,
中, ![]() 平分
平分 ![]() ,
, ![]() 于点
于点 ![]() .
.
(1)求 ![]() 的度数.
的度数.
(2)求证: ![]() .
.
【答案】
(1)解:∵ ![]()
∴∠ABC=45°
∵BD平分∠ABC
∴∠ABD= ![]() ∠ABC=22.5°
∠ABC=22.5°
在△ABD和△ECD中,∠E=∠A,∠CDE=∠BDA
∴∠ECD=∠ABD=22.5°
(2)证明:如图所示,延长BA,CE交于点F, 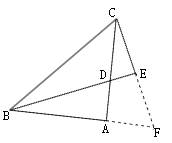
∵∠ABD+∠ADB=90°,∠CDE+∠ACF=90°,
∴∠ABD=∠ACF, 又∵AB=AC,
在Rt△ABD和Rt△ACF中 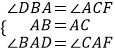
∴Rt△ABD≌Rt△ACF,
∴BD=CF,
在Rt△FBE和Rt△CBE中 ∵BD平分∠ABC,
∴∠BCF=∠F, ∵∠BEC=90°
∴∠BEF=∠BEC=90°
∵BE=BE
∴Rt△FBE≌Rt△CBE
∴EF=EC,
∴CF=2CE,
即BD=2CE
【解析】(1)根据等腰直角三角形的性质及三角形内角和定理求出∠ABC的度数,再根据角平分线的定义求出∠ABD的度数,根据三角形内角和定理及对顶角的性质即可求出∠ECD 的度数。
(2)根据BD平分∠ABC及CE⊥BE,因此添加辅助线:延长BA,CE交于点F,先证明Rt△ABD≌Rt△ACF,得出BD=CF,再证明Rt△FBE≌Rt△CBE ,得出EF=EC,得出CF=2CE,从而证得BD=2CE。


科目:初中数学 来源: 题型:
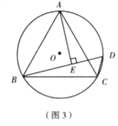
【题目】阿基米德折弦定理:如图1,AB和BC是⊙O的两条弦(即折线ABC是圆的一条折弦),BC>AB,M是![]() 的中点,则从M向BC所作垂线的垂足D是折弦ABC的中点,即CD=AB+BD.
的中点,则从M向BC所作垂线的垂足D是折弦ABC的中点,即CD=AB+BD.
下面是运用“截长法”证明CD=AB+BD的部分证明过程.
证明:如图2,在CB上截取CG=AB,连接MA,MB,MC和MG.
∵M是![]() 的中点,
的中点,
∴MA=MC
任务:(1)请按照上面的证明思路,写出该证明的剩余部分;
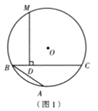
(2)填空:如图(3),已知等边△ABC内接于⊙O,AB=2,D为⊙O上 一点, ![]() ,AE⊥BD与点E,则△BDC的周长是 .
,AE⊥BD与点E,则△BDC的周长是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某年级组织学生参加夏令营,分为甲、乙、丙三组进行活动.下面两幅统计图反映了学生报名参加夏令营的情况.请你根据图中的信息回答下列问题:![]()
![]()
报名人数分布直方图 报名人数扇形统计图
(1)求该年级报名参加本次活动的总人数;
(2)求该年级报名参加乙组的人数,并补全频数分布直方图;
(3)根据实际情况,需从甲组抽调部分同学到丙组,使丙组人数是甲组人数的3倍,那么,应从甲组抽调多少名学生到丙组?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】命题 :①对顶角相等;②过一点有且只有一条直线与已知直线平行;③相等的角是对顶角;④同位角相等.其中错误的有 ( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O的内接四边形ACDB中,AB为直径,AC:BC=1:2,点D为![]() 的中点,BE⊥CD垂足为E.
的中点,BE⊥CD垂足为E.
(1)求∠BCE的度数;
(2)求证:D为CE的中点;

(3)连接OE交BC于点F,若AB=![]() ,求OE的长度.
,求OE的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】通过类比联想、引申拓展研究典型题目,可达到解一题知一类的目的.下面是一个案例.
原题:如图①,点 ![]() 分别在正方形
分别在正方形 ![]() 的边
的边 ![]() 上,
上, ![]() ,连接
,连接 ![]() ,则
,则 ![]() ,试说明理由.
,试说明理由.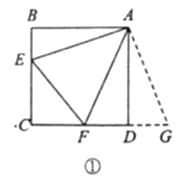
(1)思路梳理
因为 ![]() ,所以把
,所以把 ![]() 绕点
绕点 ![]() 逆时针旋转90°至
逆时针旋转90°至 ![]() ,可使
,可使 ![]() 与
与 ![]() 重合.因为
重合.因为 ![]() ,所以
,所以 ![]() ,点
,点 ![]() 共线.
共线.
根据 , 易证 ![]() , 得
, 得 ![]() .请证明.
.请证明.
(2)类比引申
如图②,四边形 ![]() 中,
中, ![]() ,
, ![]() ,点
,点 ![]() 分别在边
分别在边 ![]() 上,
上, ![]() .若
.若 ![]() 都不是直角,则当
都不是直角,则当 ![]() 与
与 ![]() 满足等量关系时,
满足等量关系时, ![]() 仍然成立,请证明.
仍然成立,请证明.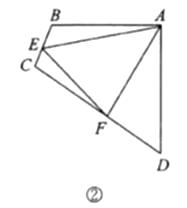
(3)联想拓展
如图③,在 ![]() 中,
中, ![]() ,点
,点 ![]() 均在边
均在边 ![]() 上,且
上,且 ![]() .猜想
.猜想 ![]() 应满足的等量关系,并写出证明过程.
应满足的等量关系,并写出证明过程.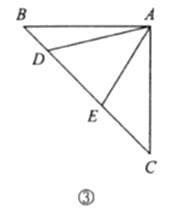
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年3月,我市某中学举行了“爱我中国朗诵比赛”活动,根据学生的成绩划分为A、B、C、D四个等级,并绘制了不完整的两种统计图.根据图中提供的信息,回答下列问题:
(1)参加朗诵比赛的学生共有 人,并把条形统计图补充完整;
(2)扇形统计图中,m= ,n= ;C等级对应扇形有圆心角为 度;
(3)学校欲从获A等级的学生中随机选取2人,参加市举办的朗诵比赛,请利用列表法或树形图法,求获A等级的小明参加市朗诵比赛的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次新冠病毒防疫知识竞赛有25道题,评委会决定:答对一道题得4分,答错或不答一题扣1分,在这次知识竞赛中,小明被评为优秀(85分或85分以上),那么小明至少答对了__________道题.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com