Question

【题目】如图，已知AB是⊙O的直径，P是BA延长线上一点，PC切⊙O于点C，CG是⊙O的弦，CG⊥AB，垂足为D．

（1）求证：∠PCA=∠ABC．

（2）过点A作AE∥PC交⊙O于点E，交CD于点F，连接BE，若cos∠P=，CF=10，求BE的长．

Answer 1

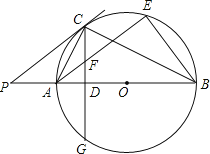
【答案】（1）见解析；（2）24．

【解析】

（1）连接半径OC，根据切线的性质得：OC⊥PC，由圆周角定理得：∠ACB=90°，所以∠PCA=∠OCB，再由同圆的半径相等可得：∠OCB=∠ABC，从而得结论；

（2）先证明∠CAF=∠ACF，则AF=CF=10，根据cos∠P=cos∠FAD=，可得AD=8，FD=6，得CD=CF+FD=16，设OC=r，OD=r-8，根据勾股定理列方程可得r的值，再由三角函数cos∠EAB=，可得AE的长，从而计算BE的长；

（1）证明：连接OC，交AE于H，

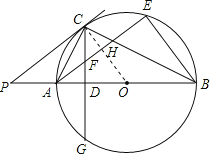
∵PC是⊙O的切线，

∴OC⊥PC，

∴∠PCO=90°，

∴∠PCA+∠ACO=90°，

∵AB是⊙O的直径，

∴∠ACB=90°，

∴∠ACO+∠OCB=90°，

∴∠PCA=∠OCB，

∵OC=OB，

∴∠OCB=∠ABC，

∴∠PCA=∠ABC；

（2）∵AE∥PC，

∴∠CAF=∠PCA，

∵AB⊥CG，

∴，

∴∠ACF=∠ABC，

∵∠ABC=∠PCA，

∴∠CAF=∠ACF，

∴AF=CF=10，

∵AE∥PC，

∴∠P=∠FAD，

∴cos∠P=cos∠FAD=，

在Rt△AFD中，cos∠FAD=，AF=10，

∴AD=8，

∴FD==6，

∴CD=CF+FD=16，

在Rt△OCD中，设OC=r，OD=r-8，

r2=（r-8）2+162，

r=20，

∴AB=2r=40，

∵AB是直径，

∴∠AEB=90°，

在Rt△AEB中，cos∠EAB=，AB=40，

∴AE=32，

∴BE==24．