
【题目】如图,反比例函数y=![]() 的图象与一次函数y=kx+4的图象在第一象限的交点于P,过点P作x轴,y轴垂线分别交于A,B两点,且函数y=kx+4的图象分别交x轴、y轴于点C,D,已知S△OCD=2,OA=2OC.
的图象与一次函数y=kx+4的图象在第一象限的交点于P,过点P作x轴,y轴垂线分别交于A,B两点,且函数y=kx+4的图象分别交x轴、y轴于点C,D,已知S△OCD=2,OA=2OC.
(1)点D的坐标为______;
(2)求一次函数解析式及m的值;
(3)写出当x>0时,不等式kx+4>![]() 的解集.
的解集.
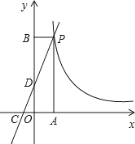
【答案】(1) (0,4);(2) 一次函数解析式为y=4x+4,m的值为24;(3) x>2.
【解析】
(1)根据一次函数y=kx+4的图象就可知它与y轴的交点D的坐标;
(2)根据S△OCD=2,可求出OC的长,得到C点、P点坐标,即可求出一次函数解析式及m的值;
(3)不等式kx+4>![]() ,可根据图象求出直线在双曲线上方时对应的x的取值范围,也就是不等式kx+4>
,可根据图象求出直线在双曲线上方时对应的x的取值范围,也就是不等式kx+4>![]() 的解集.
的解集.
解:(1)对于一次函数y=kx+4,
当x=0时,y=4
于是可知点D的坐标为(0,4).
故答案为(0,4).
(2)由(1)知OD=4,而S△OCD=2
即:![]() ×OC×OD=2
×OC×OD=2
∴OC=1,即点C的坐标为(-1,0)
将C(-1,0)代入一次函数y=kx+4中,
有-k+4=0,得k=4
∴一次函数y=kx+4的解析式为:y=4x+4
又∵OA=2OC
∴点A的坐标为(2,0)
将x=2代入y=4x+4中,得到y=12
∴点P的坐标为(2,12)
而点P在反比例函数y=![]() 的图象上,
的图象上,
则m=2×12=24
故一次函数解析式为y=4x+4,m的值为24.
(3)根据图象可知反比例函数y=![]() 的图象与一次函数y=4x+4的图象在第一象限交于P(2,12),
的图象与一次函数y=4x+4的图象在第一象限交于P(2,12),
在第一象限中,当x>2时,直线在双曲线的上方.
故当x>0时,不等式kx+4>![]() 的解集为x>2.
的解集为x>2.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】(10分)如图,一次函数![]() 与反比例函数
与反比例函数![]() 的图象交于A(1,4),B(4,n)两点.
的图象交于A(1,4),B(4,n)两点.

(1)求反比例函数的解析式;
(2)求一次函数的解析式;
(3)点P是x轴上的一动点,试确定点P并求出它的坐标,使PA+PB最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
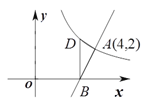
【题目】如图,直线![]() 与反比例函数
与反比例函数![]() 的图象交于点
的图象交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
(1)求![]() 的值及点
的值及点![]() 的坐标;
的坐标;
(2)过点![]() 作
作![]()
![]() 轴交反比例函数的图象于点
轴交反比例函数的图象于点![]() ,求点D的坐标和
,求点D的坐标和![]() 的面积;
的面积;
(3)观察图象,写出当x>0时不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2014年3月,某海域发生航班失联事件,我海事救援部门用高频海洋探测仪进行海上搜救,分别在A、B两个探测点探测到C处是信号发射点,已知A、B两点相距400m,探测线与海平面的夹角分别是![]() 和
和![]() ,若CD的长是点C到海平面的最短距离.
,若CD的长是点C到海平面的最短距离.
![]() 问BD与AB有什么数量关系,试说明理由;
问BD与AB有什么数量关系,试说明理由;
![]() 求信号发射点的深度
求信号发射点的深度![]() 结果精确到1m,参考数据:
结果精确到1m,参考数据:![]() ,
,![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=mx2+2mx+m-1和直线y=mx+m-1,且m≠0.
(1)求抛物线的顶点坐标;
(2)试说明抛物线与直线有两个交点;
(3)已知点T(t,0),且-1≤t≤1,过点T作x轴的垂线,与抛物线交于点P,与直线交于点Q,当0<m≤3时,求线段PQ长的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,点D是AB边的中点,过D作DE⊥BC于点E,点P是边BC上的一个动点,AP与CD相交于点Q.当AP+PD的值最小时,AQ与PQ之间的数量关系是( )

A.AQ= PQ B.AQ=3PQ C.AQ=![]() PQ D.AQ=4PQ
PQ D.AQ=4PQ
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E,过点D作DF⊥AC,垂足为F.
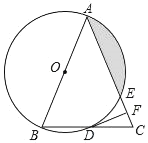
(1)求证:DF为⊙O的切线;
(2)若![]() ,∠CDF=22.5°,求阴影部分的面积.
,∠CDF=22.5°,求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
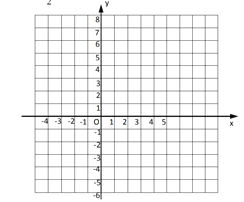
【题目】小明研究一函数的性质,下表是该函数的几组对应值:

![]() 在平面直角坐标系中,描出以上表格中的各点,根据描出的点,画出该函数图像
在平面直角坐标系中,描出以上表格中的各点,根据描出的点,画出该函数图像
![]() 根据所画函数图像,写出该函数的一条性质: .
根据所画函数图像,写出该函数的一条性质: .
![]() 根据图像直接写出该函数的解析式及自变量的取值范围: ;
根据图像直接写出该函数的解析式及自变量的取值范围: ;
![]() 若一次函数
若一次函数![]() 与该函数图像有三个交点,则
与该函数图像有三个交点,则![]() 的范围是 .
的范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:各类方程的解法
求解一元一次方程,根据等式的基本性质,把方程转化为x=a的形式.求解二元一次方程组,把它转化为一元一次方程来解;类似的,求解三元一次方程组,把它转化为解二元一次方程组.求解一元二次方程,把它转化为两个一元一次方程来解.求解分式方程,把它转化为整式方程来解,由于“去分母”可能产生增根,所以解分式方程必须检验.各类方程的解法不尽相同,但是它们有一个共同的基本数学思想![]() 转化,把未知转化为已知.
转化,把未知转化为已知.
用“转化”的数学思想,我们还可以解一些新的方程.例如,一元三次方程x3+x2-2x=0,可以通过因式分解把它转化为x(x2+x-2)=0,解方程x=0和x2+x-2=0,可得方程x3+x2-2x=0的解.
(1)问题:方程x3+x2-2x=0的解是x1=0,x2= ,x3= ;
(2)拓展:用“转化”思想求方程![]() 的解;
的解;
(3)应用:如图,已知矩形草坪ABCD的长AD=8m,宽AB=3m,小华把一根长为10m的绳子的一端固定在点B,沿草坪边沿BA,AD走到点P处,把长绳PB段拉直并固定在点P,然后沿草坪边沿PD、DC走到点C处,把长绳剩下的一段拉直,长绳的另一端恰好落在点C.求AP的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com