
【题目】已知抛物线y=mx2+2mx+m-1和直线y=mx+m-1,且m≠0.
(1)求抛物线的顶点坐标;
(2)试说明抛物线与直线有两个交点;
(3)已知点T(t,0),且-1≤t≤1,过点T作x轴的垂线,与抛物线交于点P,与直线交于点Q,当0<m≤3时,求线段PQ长的最大值.
【答案】(1)(-1,-1);(2)见解析;(3)PQ的最大值为6.
【解析】
(1)化为顶点式即可求顶点坐标;
(2)由y=mx2+2mx+m-1和y=mx+m-1可得:mx2+2mx+m-1=mx+m-1,整理得,mx(x+1)=0,即可知抛物线与直线有两个交点;
(3)由(2)可得:抛物线与直线交于(-1,-1)和(0,m-1)两点,点P的坐标为(t,mt2+2mt+m-1),点Q的坐标为(t,mt+m-1). 故分两种情况进行讨论:①如图1,当-1≤t≤0时;②如图2,当0<t≤1时,求出对应的最大值即可.
解:(1)∵y=mx2+2mx+m-1=m(x+1)2-1,
∴抛物线的顶点坐标为(-1,-1).
(2)由y=mx2+2mx+m-1和y=mx+m-1可得:mx2+2mx+m-1=mx+m-1,
mx2+mx=0,mx(x+1)=0,
∵m≠0,
∴x1=0,x2=-1.
∴抛物线与直线有两个交点.
(3)由(2)可得:抛物线与直线交于(-1,-1)和(0,m-1)两点,
点P的坐标为(t,mt2+2mt+m-1),点Q的坐标为(t,mt+m-1).
①如图1,当-1≤t≤0时,PQ=![]() =
=![]() .
.
∵m>0,
当![]() 时,PQ有最大值,且最大值为
时,PQ有最大值,且最大值为![]() .
.
∵0<m≤3,∴![]() ≤
≤![]() ,即PQ的最大值为
,即PQ的最大值为![]() .
.
②如图2,当0<t≤1时,PQ=![]() =
=![]() .
.
∵m>0,
∴当t=1时,PQ有最大值,且最大值为2m.
∵0<m≤3,
∴0<2m≤6,即PQ的最大值为6.
综上所述,PQ的最大值为6.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】下面是小芸设计的“过圆外一点作已知圆的切线”的尺规作图过程.
已知:⊙O 及⊙O 外一点 P.
求作:⊙O 的一条切线,使这条切线经过点 P.
作法:①连接 OP,作 OP 的垂直平分线 l,交 OP 于点 A;
②以 A 为圆心,AO 为半径作圆,交⊙O 于点 M;
③作直线 PM,则直线 PM 即为⊙O 的切线.

根据小芸设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明:
证明:连接 OM,
由作图可知,A 为 OP 中点,
∴OP 为⊙A 直径,
∴∠ =90°( )(填推理的依据)
即 OM⊥PM.
又∵点 M 在⊙O 上,
∴PM 是⊙O 的切线.( )(填推理的依据)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是
是![]() 的直径,点
的直径,点![]() 在
在![]() 上,点
上,点![]() 是
是![]() 上一动点,且与点
上一动点,且与点![]() 分别位于直径
分别位于直径![]() 的两侧,
的两侧,![]() ,过点
,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ;
;

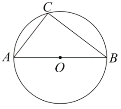
(1)当点![]() 运动到什么位置时,
运动到什么位置时,![]() 恰好是
恰好是![]() 的切线?画出图形并加以说明.
的切线?画出图形并加以说明.
(2)若点![]() 与点
与点![]() 关于直径
关于直径![]() 对称,且
对称,且![]() ,画出图形求此时
,画出图形求此时![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
问题情境
在综合与实践课上,同学们以“三角形的折叠”为主题开展数学活动.
操作发现
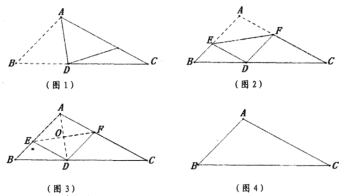
“杨辉”小组的同学用一张钝角三角形纸片![]() ,
,![]() 为钝角,进行了如下操作:
为钝角,进行了如下操作:
第一步:如图1,折出![]() 的角平分线
的角平分线![]() ;
;
第二步:如图2,展平纸片,再次折叠该三角形纸片,使预点![]() 与点
与点![]() 重合,拆痕
重合,拆痕![]() 分别与
分别与![]() ,
,![]() 交于点
交于点![]() ,
,![]() ;
;
第三步:如图3,再次展平纸片,连接![]() ,
,![]() ,可得四边形
,可得四边形![]() .
.
(1)在图4的![]() 中利用尺规作出折痕
中利用尺规作出折痕![]() ,
,![]() ;
;
(要求:保留作图痕迹,不写作法)
实践探究
(2)试判断图3中四边形![]() 的形状,并写出证明过程;
的形状,并写出证明过程;
深入探究
(3)“陈景润”小组的同学突发奇想,在“杨辉”小组同学操作的基础上设计了这样一个问题:在图3中,连接![]() ,分别交
,分别交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,若
,若![]() ,
,![]() ,利用相似三角形的知识可以求出
,利用相似三角形的知识可以求出![]() 的长.请你写出求解过程.
的长.请你写出求解过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,以Rt△ABC的斜边BC为一边在△ABC的同侧作正方形BCEF,设正方形的中心为O,连接AO,如果AB=4,AO=6![]() ,那么AC=_____.
,那么AC=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
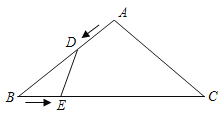
【题目】如图所示,在等腰△ABC中,AB=AC=10cm,BC=16cm.点D由点A出发沿AB方向向点B匀速运动,同时点E由点B出发沿BC方向向点C匀速运动,它们的速度均为1cm/s.连接DE,设运动时间为t(s)(0<t<10),解答下列问题:
(1)当t为何值时,△BDE的面积为7.5cm2;
(2)在点D,E的运动中,是否存在时间t,使得△BDE与△ABC相似?若存在,请求出对应的时间t;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义一种对正整数n的“F”运算:①当n为奇数时,F(n)=3n+1;②当n为偶数时,F(n)=![]() (其中k是使F(n)为奇数的正整数)……,两种运算交替重复进行,例如,取n=24,则:
(其中k是使F(n)为奇数的正整数)……,两种运算交替重复进行,例如,取n=24,则:

若n=24,则第2019次“F”运算的结果是( )
A.4B.1C.2018D.42018
查看答案和解析>>
科目:初中数学 来源: 题型:
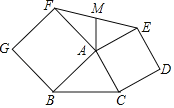
【题目】已知:如图,在△ABC中,cos∠ABC=![]() ,sin∠ACB=
,sin∠ACB=![]() ,AC=2,分别以AB,AC为边向△ABC形外作正方形ABGF和正方形ACDE,连接EF,点M是EF的中点,连接AM,则△AEF的面积为_____,AM的长为_____.
,AC=2,分别以AB,AC为边向△ABC形外作正方形ABGF和正方形ACDE,连接EF,点M是EF的中点,连接AM,则△AEF的面积为_____,AM的长为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com