练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】定义一种对正整数n的“F”运算：①当n为奇数时，F（n）=3n+1；②当n为偶数时，F（n）=（其中k是使F（n）为奇数的正整数）……，两种运算交替重复进行，例如，取n=24，则：

    若n=24，则第2019次“F”运算的结果是（ ）

    A.4B.1C.2018D.42018

    【答案】B

    【解析】

    计算出n＝24时第1、2、3、4、5、6、7次运算的结果，找出规律再进行解答即可．

    解：解：若n＝24，
    第1次结果为3，第2次结果是10，第3次结果为5，第4次结果为16，第5次结果为1，第6次结果为4，第7次结果为1，……
    可以看出，从第5次开始，结果就只是1，4两个数轮流出现，
    且当次数为偶数时，结果是4；次数是奇数时，结果是1，
    而2019次是奇数，因此最后结果是1．
    故答案为：B．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

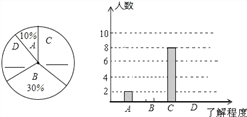
    【题目】2013年5月31日是第26个“世界无烟日”，校学生会书记小明同学就“戒烟方式”的了解程度对本校九年级学生进行了一次随机问卷调查，如图是他采集数据后绘制的两幅不完整的统计图（A：了解较多，B：不了解，C：了解一点，D：非常了解）．请你根据图中提供的信息解答以下问题：

    （1）在扇形统计图中的横线上填写缺失的数据，并把条形统计图补充完整．

    （2）2013年该初中九年级共有学生400人，按此调查，可以估计2013年该初中九年级学生中对戒烟方式“了解较多”以上的学生约有多少人？

    （3）在问卷调查中，选择“A”的是1名男生，1名女生，选择“D”的有4人且有2男2女．校学生会要从选择“A、D”的问卷中，分别抽一名学生参加活动，请你用列表法或树状图求出恰好是一名男生一名女生的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知抛物线y=mx2+2mx+m-1和直线y=mx+m-1，且m≠0．

    （1）求抛物线的顶点坐标；

    （2）试说明抛物线与直线有两个交点；

    （3）已知点T（t，0），且-1≤t≤1，过点T作x轴的垂线，与抛物线交于点P，与直线交于点Q，当0＜m≤3时，求线段PQ长的最大值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如下表，从左边第一个格子开始向右数，在每个小格子中都填入一个整数，使得其中仼意三个相邻格子中所填整数之和都相等．

    5

    4

    ……

    （1）可求得_____；_____；_____．

    （2）第2019个格子中的数为______；

    （3）前2020个格子中所填整数之和为______．

    （4）前个格子中所填整数之和是否可能为2020？若能，求出的值，若不能，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

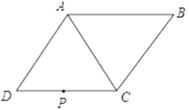
    【题目】如图，在菱形ABCD中，∠ADC＝60°，CD＝4cm，P为CD的中点．

    （1）在AC上找一点Q，使DQ+PQ的值最小（保留画图痕迹，不写画法，不必说理）；

    （2）求出（1）中DQ+PQ的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

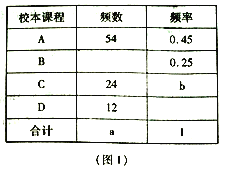
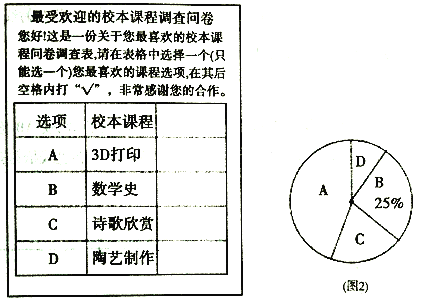
    【题目】某校开设了“3D”打印、数学史、诗歌欣赏、陶艺制作四门校本课程，为了解学生对这四门校本课程的喜爱情况，对学生进行了随机问卷调查（问卷调查表如图所示），将调查结果整理后绘制了（图1）、（图2）两幅均不完整的统计图．

    请您根据图中提供的信息回答下列问题：

    （1）统计图中的a= ，b= ；

    （2）“D”对应扇形的圆心角为 度；

    （3）根据调查结果，请您估计该校1200名学生中最喜欢“数学史”校本课程的人数；

    （4）小明和小亮参加校本课程学习，若每人从“A”、“B”、“C”三门校本课程中随机选取一门，请用画树状图或列表格的方法，求两人恰好选中同一门校本课程的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】甲、乙、丙、丁四位同学进行一次乒乓球单打比赛，要从中选出两位同学打第一场比赛.

    （1）请用树状图法或列表法，求恰好选中甲、乙两位同学的概率.

    （2）若已确定甲打第一场，再从其余三位同学中随机选取一位，求恰好选中乙同学的概率.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

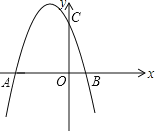
    【题目】如图，抛物线y＝ax2+bx+3与x轴交于A（﹣3，0），B（l，0）两点，与y轴交于点C．

    （1）求抛物线的解析式；

    （2）点P是抛物线上的动点，且满足S△PAO＝2S△PCO，求出P点的坐标；

    （3）连接BC，点E是x轴一动点，点F是抛物线上一动点，若以B、C、E、F为顶点的四边形是平行四边形时，请直接写出点F的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

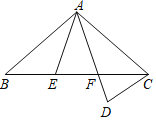
    【题目】如图，△ABC中，AB=AC，点E，F在边BC上，BE=CF，点D在AF的延长线上，AD=AC．

    （1）求证：△ABE≌△ACF；

    （2）若∠BAE=30°，则∠ADC=　 　°．

    查看答案和解析>>

    同步练习册答案