
【题目】如下表,从左边第一个格子开始向右数,在每个小格子中都填入一个整数,使得其中仼意三个相邻格子中所填整数之和都相等.
|
|
|
| 5 | 4 | …… |
(1)可求得![]() _____;
_____;![]() _____;
_____;![]() _____.
_____.
(2)第2019个格子中的数为______;
(3)前2020个格子中所填整数之和为______.
(4)前![]() 个格子中所填整数之和是否可能为2020?若能,求出
个格子中所填整数之和是否可能为2020?若能,求出![]() 的值,若不能,请说明理由.
的值,若不能,请说明理由.
【答案】(1)![]() ,
,![]() ,
,![]() ;(2)4;(3)665;(4)能;前6060,6071或6085个格子中所填整数之和为2020.
;(2)4;(3)665;(4)能;前6060,6071或6085个格子中所填整数之和为2020.
【解析】
(1)根据题意,直接求出x,y,z的值,即可;
(2)由题意得:表格中的数字是3个以循环,进而即可求解;
(3)由“表格中的数字是3个以循环” ,2020÷3=673…1,即可求解;
(4)分三种情况,分类讨论,即可求解.
(1)由题意得:-8+x+y=x+y+z,解得:![]() ,
,
x+y+z= y+z+5,解得:![]() ,
,
∴表格中的数字是3个以循环,即:-8,5,4,-8,5,4,…,
∴![]() .
.
故答案是:![]() ,
,![]() ,
,![]() ;
;
(2)∵表格中的数字是3个以循环,即:-8,5,4,-8,5,4,…,2019÷3=673,
∴第2019个格子中的数为:4.
故答案是:4;
(3)∵2020÷3=673…1,-8+5+4=1,
∴前2020个格子中所填整数之和为:673×1+(-8)=665.
故答案是:665.
(4)能,理由如下:
①![]() ,
,
![]() ;
;
②∵![]() ,
,
∴![]() ;
;
③∵![]() ,
,
∴![]() ;
;
综上所述:前6060或6071或6085个格子中所填整数之和为2020.


科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AC,BD相交于点O,点E是OA的中点,连接BE并延长交AD于点F,已知S△AEF=4,则下列结论:①![]() ;②S△BCE=36;③S△ABE=12;④△AEF~△ACD,其中一定正确的是( )
;②S△BCE=36;③S△ABE=12;④△AEF~△ACD,其中一定正确的是( )

A. ①②③④ B. ①④ C. ②③④ D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
问题情境
在综合与实践课上,同学们以“三角形的折叠”为主题开展数学活动.
操作发现
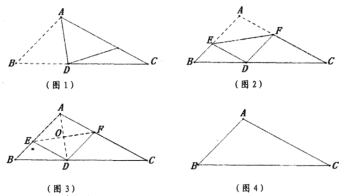
“杨辉”小组的同学用一张钝角三角形纸片![]() ,
,![]() 为钝角,进行了如下操作:
为钝角,进行了如下操作:
第一步:如图1,折出![]() 的角平分线
的角平分线![]() ;
;
第二步:如图2,展平纸片,再次折叠该三角形纸片,使预点![]() 与点
与点![]() 重合,拆痕
重合,拆痕![]() 分别与
分别与![]() ,
,![]() 交于点
交于点![]() ,
,![]() ;
;
第三步:如图3,再次展平纸片,连接![]() ,
,![]() ,可得四边形
,可得四边形![]() .
.
(1)在图4的![]() 中利用尺规作出折痕
中利用尺规作出折痕![]() ,
,![]() ;
;
(要求:保留作图痕迹,不写作法)
实践探究
(2)试判断图3中四边形![]() 的形状,并写出证明过程;
的形状,并写出证明过程;
深入探究
(3)“陈景润”小组的同学突发奇想,在“杨辉”小组同学操作的基础上设计了这样一个问题:在图3中,连接![]() ,分别交
,分别交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,若
,若![]() ,
,![]() ,利用相似三角形的知识可以求出
,利用相似三角形的知识可以求出![]() 的长.请你写出求解过程.
的长.请你写出求解过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
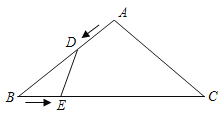
【题目】如图所示,在等腰△ABC中,AB=AC=10cm,BC=16cm.点D由点A出发沿AB方向向点B匀速运动,同时点E由点B出发沿BC方向向点C匀速运动,它们的速度均为1cm/s.连接DE,设运动时间为t(s)(0<t<10),解答下列问题:
(1)当t为何值时,△BDE的面积为7.5cm2;
(2)在点D,E的运动中,是否存在时间t,使得△BDE与△ABC相似?若存在,请求出对应的时间t;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数![]() 的图象经过点
的图象经过点![]() .
.
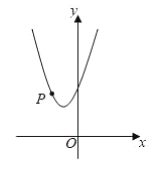
(1)求![]() 的值和图象的顶点坐标;
的值和图象的顶点坐标;
(2)点![]() 在该二次函数图象上.
在该二次函数图象上.
①当![]() 时,求
时,求![]() 的值;
的值;
②若点![]() 到
到![]() 轴的距离小于2,请根据图象直接写出
轴的距离小于2,请根据图象直接写出![]() 的取值范围;
的取值范围;
③直接写出点![]() 与直线
与直线![]() 的距离小于
的距离小于![]() 时
时![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义一种对正整数n的“F”运算:①当n为奇数时,F(n)=3n+1;②当n为偶数时,F(n)=![]() (其中k是使F(n)为奇数的正整数)……,两种运算交替重复进行,例如,取n=24,则:
(其中k是使F(n)为奇数的正整数)……,两种运算交替重复进行,例如,取n=24,则:

若n=24,则第2019次“F”运算的结果是( )
A.4B.1C.2018D.42018
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】快递公司为提高快递分拣的速度,决定购买机器人来代替人工分拣,两种型号的机器人的工作效率和价格如表:
型号 | 甲 | 乙 |
每台每小时分拣快递件数(件) | 1000 | 800 |
每台价格(万元) | 5 | 3 |
该公司计划购买这两种型号的机器人共10台,并且使这10台机器人每小时分拣快递件数总和不少于8500件
(1)设购买甲种型号的机器人x台,购买这10台机器人所花的费用为y万元,求y与x之间的关系式;
(2)购买几台甲种型号的机器人,能使购买这10台机器人所花总费用最少?最少费用是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com