
����Ŀ���ۺ���ʵ��
�����龳
���ۺ���ʵ�����ϣ�ͬѧ�����������ε��۵���Ϊ���չ��ѧ���
��������
�������С���ͬѧ��һ�Ŷ۽�������ֽƬ![]() ��
��![]() Ϊ�۽ǣ����������²�����
Ϊ�۽ǣ����������²�����
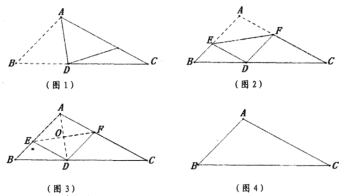
��һ������ͼ1���۳�![]() �Ľ�ƽ����
�Ľ�ƽ����![]() ��
��
�ڶ�������ͼ2��չƽֽƬ���ٴ��۵���������ֽƬ��ʹԤ��![]() ���
���![]() �غϣ����
�غϣ����![]() �ֱ���
�ֱ���![]() ��
��![]() ���ڵ�
���ڵ�![]() ��
��![]() ��
��
����������ͼ3���ٴ�չƽֽƬ������![]() ��
��![]() ���ɵ��ı���
���ɵ��ı���![]() ��
��
��1����ͼ4��![]() �����ó߹������ۺ�
�����ó߹������ۺ�![]() ��
��![]() ��
��
��Ҫ������ͼ�ۼ�����д������
ʵ��̽��
��2�����ж�ͼ3���ı���![]() ����״����д��֤�����̣�
����״����д��֤�����̣�
����̽��
��3�����¾�����С���ͬѧͻ�����룬���������С��ͬѧ�����Ļ��������������һ�����⣺��ͼ3�У�����![]() ���ֱ�
���ֱ�![]() �ڵ�
�ڵ�![]() ����
����![]() �ڵ�
�ڵ�![]() ����
����![]() ��
��![]() ���������������ε�֪ʶ�������
���������������ε�֪ʶ�������![]() �ij�������д�������̣�
�ij�������д�������̣�
���𰸡���1������������2�����Σ�֤������������3��![]() �����̼�����
�����̼�����
��������
��1������BAC�Ľ�ƽ����AD��BC���ڵ�D������AD���д�����AB����E����AC����F���ɣ�
��2�����۵���֪��![]() ��
��![]() �Ľ�ƽ���ߣ�
�Ľ�ƽ���ߣ�![]() ��
��![]() �Ĵ�ֱƽ���ߣ���ͨ����ֱƽ���ߺͽ�ƽ���ߵ����ʿɵ�
�Ĵ�ֱƽ���ߣ���ͨ����ֱƽ���ߺͽ�ƽ���ߵ����ʿɵ�![]() ��
��![]() ������֤���ı���
������֤���ı���![]() ��ƽ���ı��Σ��ٸ���
��ƽ���ı��Σ��ٸ���![]() ����֤ƽ���ı���
����֤ƽ���ı���![]() �����Σ�
������
��3������![]() ��ͨ��֤��
��ͨ��֤��![]() ���ɵ�
���ɵ�![]() ����
����![]() �����
�����![]() ���Ӷ��ó�
���Ӷ��ó�![]() ��
��
�⣺��1����ͼ��ʾ��
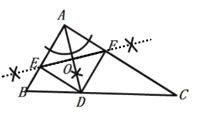
��2������
֤�������۵���֪��![]() ��
��![]() �Ľ�ƽ���ߣ�
�Ľ�ƽ���ߣ�![]() ��
��![]() �Ĵ�ֱƽ���ߣ�
�Ĵ�ֱƽ���ߣ�
��![]() ��
��![]() �Ĵ�ֱƽ����
�Ĵ�ֱƽ����
��![]() ��
��![]() ��
��
��![]() ��
��![]()
��![]() ��
��![]() �Ľ�ƽ����
�Ľ�ƽ����
��![]()
��![]() ��
��![]()
��![]() ��
��![]()
���ı���![]() ��ƽ���ı��Σ�
��ƽ���ı��Σ�
�֡�![]()
��ƽ���ı���![]() �����Σ�
������
��3������![]() ��
��
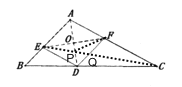
���ı���![]() Ϊ���Σ�
����
��![]() ��ֱƽ��
��ֱƽ��![]() ��
��
���![]() ��
��![]() �Ĵ�ֱƽ����
�Ĵ�ֱƽ����![]() �ϣ�
�ϣ�![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
�֡�![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס��������ֱ��A��B��������������ʻ���׳��ȳ�����Сʱ���׳�����B�غ�������ͷ��������ԭ�ٶ����ҳ�ͬ����ʻ���ҳ�����A�غ�������ԭ����Զ��B�ķ�����ʻ������һ��ʱ�������ͬʱ����C�أ�������֮��ľ���Ϊy�����ף����׳���ʻ��ʱ��ΪxСʱ��y��x֮��ĺ���ͼ����ͼ��ʾ���׳��ط�A��ʱ���ҳ�����C��________ǧ��.
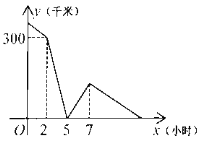
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
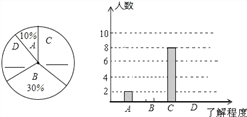
����Ŀ��2013��5��31���ǵ�26�������������ա���Уѧ�������С��ͬѧ�͡����̷�ʽ�����˽�̶ȶԱ�У���꼶ѧ��������һ������ʾ����飬��ͼ�����ɼ����ݺ���Ƶ�������������ͳ��ͼ��A���˽�϶࣬B�����˽⣬C���˽�һ�㣬D���dz��˽⣩���������ͼ���ṩ����Ϣ����������⣺
��1��������ͳ��ͼ�еĺ�������дȱʧ�����ݣ���������ͳ��ͼ����������
��2��2013��ó��о��꼶����ѧ��400�ˣ����˵��飬���Թ���2013��ó��о��꼶ѧ���жԽ��̷�ʽ���˽�϶ࡱ���ϵ�ѧ��Լ�ж����ˣ�
��3�����ʾ������У�ѡ��A������1��������1��Ů����ѡ��D������4������2��2Ů��Уѧ����Ҫ��ѡ��A��D�����ʾ��У��ֱ��һ��ѧ���μӻ���������б�������״ͼ���ǡ����һ������һ��Ů���ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������![]() ��
��![]() �ύ��
�ύ��![]() ��
��![]() ���㣬��
���㣬��![]() ��
��![]() �������ֱ��
�������ֱ��![]() ���·�����ô����˵����ȷ���ǣ� ��
���·�����ô����˵����ȷ���ǣ� ��
A.�����߿���һ������B.�����ߵĶ��㲻�����ڵ�������
C.����������ֱ֪������������D.�����ߵĶԳ��������![]() ���Ҳ�
���Ҳ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����![]() �У�
��![]() ��
��![]() ��
��![]() ����һ���㣬�Ե�
����һ���㣬�Ե�![]() Ϊ���㣬
Ϊ���㣬![]() Ϊһ��������
Ϊһ��������![]() ��ʹ
��ʹ![]() ����
����![]() ����
����![]() ��
��![]() �����dz�
�����dz�![]() Ϊ
Ϊ![]() ������������������
������������������
��1����![]() ��
��![]() ��������ϵ��
��������ϵ��
��2����ͼ2��![]() Ϊ
Ϊ![]() ����������������������
����������������������![]() ��
��![]() ��ƽ���ߣ���
��ƽ���ߣ���![]() �ڵ�
�ڵ�![]() �����ı���
�����ı���![]() ��ƽ���ı��Σ���֤��
��ƽ���ı��Σ���֤��![]() ��
��
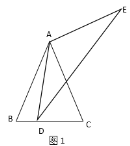
��3����ͼ3���ı���![]() �У�
��![]() ��
��![]() ����
����![]() ��
��![]() �ϣ�
�ϣ�![]() ��
��![]() B��
B��![]() ����
����![]() ��
��![]() ����
����![]() ��ֵ��
��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
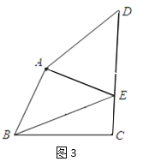
����Ŀ����ͼ�������������ABC�У���D��E�ֱ��ڱ�AC��AB�ϣ�AG��BC�ڵ�G��AF��DE�ڵ�F����EAF=��GAC��
��1����֤����ADE�ס�ABC��
��2����AD=3��AB=5����![]() ��ֵ��
��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������y=mx2+2mx+m-1��ֱ��y=mx+m-1����m��0��
��1���������ߵĶ������ꣻ
��2����˵����������ֱ�����������㣻
��3����֪��T��t��0������-1��t��1������T��x��Ĵ��ߣ��������߽��ڵ�P����ֱ�߽��ڵ�Q����0��m��3ʱ�����߶�PQ�������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����±�������ߵ�һ�����ӿ�ʼ����������ÿ��С�����ж�����һ��������ʹ�����Ё����������ڸ�������������֮�Ͷ���ȣ�
|
|
|
| 5 | 4 | ���� |
��1�������![]() _____��
_____��![]() _____��
_____��![]() _____��
_____��
��2����2019�������е���Ϊ______��
��3��ǰ2020����������������֮��Ϊ______��
��4��ǰ![]() ����������������֮���Ƿ����Ϊ2020�����ܣ����
����������������֮���Ƿ����Ϊ2020�����ܣ����![]() ��ֵ�������ܣ���˵�����ɣ�
��ֵ�������ܣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
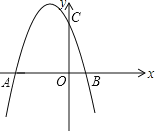
����Ŀ����ͼ��������y��ax2+bx+3��x�ύ��A����3��0����B��l��0�����㣬��y�ύ�ڵ�C��
��1���������ߵĽ���ʽ��
��2����P���������ϵĶ��㣬������S��PAO��2S��PCO�����P������ꣻ
��3������BC����E��x��һ���㣬��F����������һ���㣬����B��C��E��FΪ������ı�����ƽ���ı���ʱ����ֱ��д����F�����꣮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com