
【题目】如图,抛物线过x轴上两点A(9,0),C(-3,0),且与y轴交于点B(0,-12).
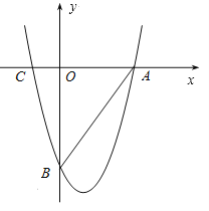
(1)求抛物线的解析式;
(2)若动点P从点A出发,以每秒2个单位沿射线AC方向运动;同时,点Q从点B出发,以每秒1个单位沿射线BA方向运动,当点P到达点C处时,两点同时停止运动.问当t为何值时,△APQ∽△AOB?
(3)若M为线段AB上一个动点,过点M作MN平行于y轴交抛物线于点N.
①是否存在这样的点M,使得四边形OMNB恰为平行四边形?若存在,求出点M的坐标;若不存在,请说明理由.
②当点M运动到何处时,四边形CBNA的面积最大?求出此时点M的坐标及四边形CBNA面积的最大值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)①不存在;②当点M运动到(
;(3)①不存在;②当点M运动到(![]() ,-6)时,四边形CBNA的面积最大,四边形CBNA面积的最大值为
,-6)时,四边形CBNA的面积最大,四边形CBNA面积的最大值为![]() .
.
【解析】
试题(1)应用待定系数法,设交点式求解;
(2)根据相似三角形的性质求解即可;
(3)①由MN=OB=12列式,根据一元二次方程根的判别式小于0得出不存在这样的点M,使得四边形OMNB恰为平行四边形结论;②求出面积关于x的二次函数关系式,应用二次函数最值原理求解即可.
试题解析:(1)因抛物线过x轴上两点A(9,0),C(-3,0),故设抛物线解析式为:![]() .
.
又∵B(0,-12) ∴![]() ,解得a=
,解得a=![]() 。
。
∴抛物线的解析式为![]() .
.
(2)∵OA=9,OB=12,∴AB=15.
∵点P的速度是每秒2个单位,点Q的速度是每秒1个单位,∴AP=2t,AQ=15-t.
又∵AC=12,∴0≤t≤6.
∵△APQ∽△AOB,∴![]() ,即
,即![]() ,解得
,解得![]() .
.
∴当![]() 时,△APQ∽△AOB.
时,△APQ∽△AOB.
(3)易求直线AB的函数关系式为![]() .
.
设点M的横坐标为x,则M(x,![]() ),N(x,
),N(x,![]() ).
).
①若四边形OMNB为平行四边形,则MN=OB=12
∴![]() ,即x2-9x+27=0.
,即x2-9x+27=0.
∵△<0,∴此方程无实数根.
∴不存在这样的点M,使得四边形OMNB恰为平行四边形.
②∵S四边形CBNA=S△ACB+S△ABN="72+" S△ABN
∵S△AOB=54,S△OBN=6x,S△OAN=![]() ·9·
·9·![]() =-2x2+12x+54
=-2x2+12x+54
∴S△ABN=S△OBN+S△OAN-S△AOB=6x+(-2x2+12x+54)-54=-2x2+18x=![]() .
.
∴当x=![]() 时,S△ABN最大值=
时,S△ABN最大值=![]() ,此时M(
,此时M(![]() ,-6)
,-6)
S四边形CBNA最大=![]() .
.


科目:初中数学 来源: 题型:
【题目】下列说法不正确的是
A. 某种彩票中奖的概率是![]() ,买1000张该种彩票一定会中奖
,买1000张该种彩票一定会中奖
B. 了解一批电视机的使用寿命适合用抽样调查
C. 若甲组数据的标准差S甲=0.31,乙组数据的标准差S乙=0.25,则乙组数据比甲组数据稳定
D. 在一个装有白球和绿球的袋中摸球,摸出黑球是不可能事件
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,每个小正方形的边长都是1的方格纸中,有线段AC和EF,点A、C、E、F都在小正方形的顶点上.
(1)在方格纸中画出一个以线段AC为对角线的正方形ABCD,所画的正方形的各顶点必须在小正方形的顶点上.
(2)在方格纸中以EF为腰画出等腰三角形△EFM,点M在小正方形的顶点上,且MF=MC.
(3)在(1)、(2)的条件下,连接MA,请直接写出线段MA的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,边AD绕点A顺时针旋转角度m(0°<m<360°),得到线段AP,连接PB,PC.当△BPC是等腰三角形时,m的值为________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某景区内从甲地到乙地的路程是![]() ,小华步行从甲地到乙地游玩,速度为
,小华步行从甲地到乙地游玩,速度为![]() ,走了
,走了![]() 后,中途休息了一段时间,然后继续按原速前往乙地,景区从甲地开往乙地的电瓶车每隔半小时发一趟车,速度是
后,中途休息了一段时间,然后继续按原速前往乙地,景区从甲地开往乙地的电瓶车每隔半小时发一趟车,速度是![]() ,若小华与第1趟电瓶车同时出发,设小华距乙地的路程为
,若小华与第1趟电瓶车同时出发,设小华距乙地的路程为![]() ,第
,第![]() 趟电瓶车距乙地的路程为
趟电瓶车距乙地的路程为![]() ,
,![]() 为正整数,行进时间为
为正整数,行进时间为![]() .如图画出了
.如图画出了![]() ,
,![]() 与
与![]() 的函数图象.
的函数图象.
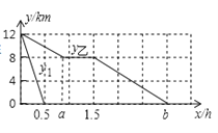
(1)观察图,其中![]() ,
,![]() ;
;
(2)求第2趟电瓶车距乙地的路程![]() 与
与![]() 的函数关系式;
的函数关系式;
(3)当![]() 时,在图中画出
时,在图中画出![]() 与
与![]() 的函数图象;并观察图象,得出小华在休息后前往乙地的途中,共有 趟电瓶车驶过.
的函数图象;并观察图象,得出小华在休息后前往乙地的途中,共有 趟电瓶车驶过.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在水果销售旺季,某水果店购进一优质水果,进价为 20 元/千克,售价不低于 20 元/千克,且不超过 32 元/千克,根据销售情况,发现该水果一天的销售量 y(千克)与该天的售价 x(元/千克)满足如下表所示的一次函数关系.
销售量 y(千克) | … | 34.8 | 32 | 29.6 | 28 | … |
售价 x(元/千克) | … | 22.6 | 24 | 25.2 | 26 | … |
(1)某天这种水果的售价为 23.5 元/千克,求当天该水果的销售量.
(2)如果某天销售这种水果获利 150 元,那么该天水果的售价为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农户承包荒山种了44棵苹果树.现在进入第三年收获期.收获时,先随意摘了5棵树上的苹果,称得每棵树摘得的苹果重量如下(单位:千克)35 35 34 39 37
(1)在这个问题中,总体指的是?个体指的是?样本是?样本容量是?
(2)试根据样本平均数去估计总体情况,你认为该农户可收获苹果大约多少千克?
查看答案和解析>>
科目:初中数学 来源: 题型:
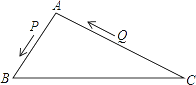
【题目】如图,△ABC中,AB=8厘米,AC=16厘米,点P从A出发,以每秒2厘米的速度向B运动,点Q从C同时出发,以每秒3厘米的速度向A运动,其中一个动点到端点时,另一个动点也相应停止运动,那么,当以A、P、Q为顶点的三角形与△ABC相似时,运动时间是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
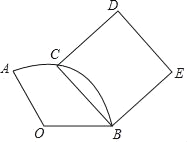
【题目】如图,已知扇形AOB中,OA=3,∠AOB=120°,C是在![]() 上的动点.以BC为边作正方形BCDE,当点C从点A移动至点B时,点D经过的路径长是_____.
上的动点.以BC为边作正方形BCDE,当点C从点A移动至点B时,点D经过的路径长是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com