
ЎҫМвДҝЎҝТСЦӘ ![]() ЦРЈ¬
ЦРЈ¬ ![]() .өг
.өг ![]() ҙУөг
ҙУөг ![]() іц·ўСШПЯ¶О
іц·ўСШПЯ¶О ![]() ТЖ¶ҜЈ¬Н¬Кұөг
ТЖ¶ҜЈ¬Н¬Кұөг ![]() ҙУөг
ҙУөг ![]() іц·ўСШПЯ¶О
іц·ўСШПЯ¶О ![]() өДСУіӨПЯТЖ¶ҜЈ¬өг
өДСУіӨПЯТЖ¶ҜЈ¬өг ![]() Ўў
Ўў ![]() ТЖ¶ҜөДЛЩ¶ИПаН¬Ј¬
ТЖ¶ҜөДЛЩ¶ИПаН¬Ј¬ ![]() УлЦұПЯ
УлЦұПЯ ![]() ПаҪ»УЪөг
ПаҪ»УЪөг ![]() .
.
ЈЁ1Ј©ИзНјўЩЈ¬өұөг ![]() ОӘ
ОӘ ![]() өДЦРөгКұЈ¬Зу
өДЦРөгКұЈ¬Зу ![]() өДіӨЈ»
өДіӨЈ»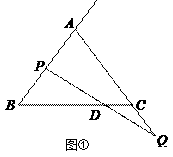
ЈЁ2Ј©ИзНјўЪЈ¬№эөг ![]() ЧчЦұПЯ
ЧчЦұПЯ ![]() өДҙ№ПЯЈ¬ҙ№ЧгОӘ
өДҙ№ПЯЈ¬ҙ№ЧгОӘ ![]() Ј¬өұөг
Ј¬өұөг ![]() Ўў
Ўў ![]() ФЪТЖ¶ҜөД№эіМЦРЈ¬Йи
ФЪТЖ¶ҜөД№эіМЦРЈ¬Йи ![]() Ј¬
Ј¬ ![]() КЗ·сОӘіЈКэЈҝИфКЗЗлЗуіц
КЗ·сОӘіЈКэЈҝИфКЗЗлЗуіц ![]() өДЦөЈ¬ИфІ»КЗЗлЛөГчАнУЙ.
өДЦөЈ¬ИфІ»КЗЗлЛөГчАнУЙ.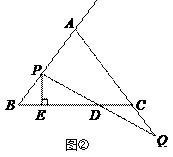
ЈЁ3Ј©ИзНјўЫЈ¬EОӘBCөДЦРөгЈ¬ЦұПЯCHҙ№ЦұУЪЦұПЯADЈ¬ҙ№ЧгОӘөгHЈ¬Ҫ»AEөДСУіӨПЯУЪөгMЈ»ЦұПЯBFҙ№ЦұУЪЦұПЯADЈ¬ҙ№ЧгОӘFЈ»ХТіцНјЦРУлBDПаөИөДПЯ¶ОЈ¬ІўЦӨГч.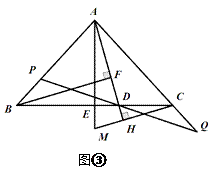
Ўҫҙр°ёЎҝ
ЈЁ1Ј©ҪвЈәИзНјЈ¬№эPөгЧчPFЎОACҪ»BCУЪFЈ¬
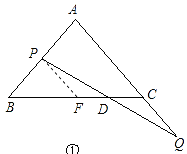
ЎЯөгPәНөгQН¬Кұіц·ўЈ¬ЗТЛЩ¶ИПаН¬Ј¬
ЎаBP=CQЈ¬
ЎЯPFЎОAQЈ¬
ЎаЎПPFB=ЎПACBЈ¬ЎПDPF=ЎПCQDЈ¬
УЦЎЯAB=ACЈ¬
ЎаЎПB=ЎПACBЈ¬
ЎаЎПB=ЎПPFBЈ¬
ЎаBP=PFЈ¬
ЎаPF=CQЈ¬УЦЎПPDF=ЎПQDCЈ¬
ЎаЎчPFDЎХЎчQCDЈ¬
ЎаDF=CD= ![]() CFЈ¬
CFЈ¬
УЦТтPКЗABөДЦРөгЈ¬PFЎОAQЈ¬
ЎаFКЗBCөДЦРөгЈ¬јҙFC= ![]() BC=6Ј¬
BC=6Ј¬
ЎаCD= ![]() CF=3
CF=3
ЈЁ2Ј©ҪвЈә ![]() ОӘ¶ЁЦө.
ОӘ¶ЁЦө.
ИзНјўЪЈ¬өгPФЪПЯ¶ОABЙПЈ¬№эөгPЧчPFЎОACҪ»BCУЪFЈ¬
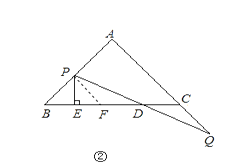
ТЧЦӘЎчPBFОӘөИСьИэҪЗРОЈ¬
ЎЯPEЎНBF
ЎаBE= ![]() BF
BF
ЎЯТЧөГЎчPFDЎХЎчQCD
ЎаCD= ![]()
Ўа ![]()
ЈЁ3Ј©ҪвЈәBD=AM
ЦӨГчЈәЎЯ ![]()
Ўа ![]()
Ўа ![]()
ЎЯEОӘBCөДЦРөг
Ўа ![]()
Ўа ![]() ,
, ![]()
Ўа ![]() Ј¬
Ј¬ ![]()
ЎЯAHЎНCM
Ўа ![]()
ЎЯ ![]()
Ўа ![]()
Ўа ![]() ЎХ
ЎХ ![]() (ASA)
(ASA)
Ўа ![]()
Ўа ![]()
јҙЈә ![]()
ЎҫҪвОцЎҝЈЁ1Ј©ёщҫЭТСЦӘҝЙЦӘBP=CQЈ¬ФЩёщҫЭPFЎОAQј°AB=ACЈ¬ЦӨГчЎПB=ЎПPFBЈ¬өГіцBP=PFЈ¬ЦӨөГPF=CQЈ¬И»әуёщҫЭҪЗҪЗұЯЦӨГчЎчPFDЎХЎчQCDЈ¬өГіцDF=CD=![]() CFЈ¬ёщҫЭТСЦӘPКЗABөДЦРөгЈ¬PFЎОAQЈ¬ЦӨГчөгFКЗBCөДЦРөгЈ¬ЗуіцCFөДіӨЈ¬јҙҝЙЗуіцCDөДіӨЎЈ
CFЈ¬ёщҫЭТСЦӘPКЗABөДЦРөгЈ¬PFЎОAQЈ¬ЦӨГчөгFКЗBCөДЦРөгЈ¬ЗуіцCFөДіӨЈ¬јҙҝЙЗуіцCDөДіӨЎЈ
ЈЁ2Ј©өгPФЪПЯ¶ОABЙПЈ¬№эөгPЧчPFЎОACҪ»BCУЪFЈ¬ПИЦӨГчЎчPBFОӘөИСьИэҪЗРОЈ¬ёщҫЭPEЎНBFЈ¬өГіцBEУлПЯ¶ОBFөДКэБҝ№ШПөЈ¬ФЩЦӨГчЎчPFDЎХЎчQCD Ј¬ҪбәПCD= ![]() C FЈ¬И»әуёщҫЭB E + C D =
C FЈ¬И»әуёщҫЭB E + C D =![]() BCЈ¬јҙҝЙөГіцҪбВЫЎЈ
BCЈ¬јҙҝЙөГіцҪбВЫЎЈ
ЈЁ3Ј©ПИёщҫЭ№ҙ№Й¶ЁАнөДДж¶ЁАнЦӨГчҰӨABCКЗөИСьЦұҪЗИэҪЗРОЈ¬ ФЩёщҫЭEОӘBCөДЦРөгЈ¬ИҘЦӨГчAE=ECЈ¬ЎПEAD = ЎПECMЈ¬И»әуЦӨГчЎчAEDЎХЎчCEMЈ¬өГіцDE=MEЈ¬ёщҫЭBD=DE+BE=AE+ME=AMЎЈјҙҝЙөГіцҪбВЫЎЈ


 ІҪІҪёЯҙпұкҫнПөБРҙр°ё
ІҪІҪёЯҙпұкҫнПөБРҙр°ё
| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝДі№Өі§УРјЧЦЦФӯБП![]() Ј¬ТТЦЦФӯБП
Ј¬ТТЦЦФӯБП![]() Ј¬ПЦУГБҪЦЦФӯБПЙъІъҙҰ
Ј¬ПЦУГБҪЦЦФӯБПЙъІъҙҰ![]() БҪЦЦІъЖ·№І
БҪЦЦІъЖ·№І![]() јюЈ¬ТСЦӘЙъІъГҝјю
јюЈ¬ТСЦӘЙъІъГҝјю![]() ІъЖ·РијЧЦЦФӯБП
ІъЖ·РијЧЦЦФӯБП![]() Ј¬ТТЦЦФӯБП
Ј¬ТТЦЦФӯБП![]() Ј¬ЗТГҝјю
Ј¬ЗТГҝјю![]() ІъЖ·ҝЙ»сөГ
ІъЖ·ҝЙ»сөГ![]() ФӘЈ»ЙъІъГҝјю
ФӘЈ»ЙъІъГҝјю![]() ІъЖ·јЧЦЦФӯБП
ІъЖ·јЧЦЦФӯБП![]() Ј¬ТТЦЦФӯБП
Ј¬ТТЦЦФӯБП![]() Ј¬ЗТГҝјю
Ј¬ЗТГҝјю![]() ІъЖ·ҝЙ»сАыИу
ІъЖ·ҝЙ»сАыИу![]() ФӘЈ¬ЙиЙъІъ
ФӘЈ¬ЙиЙъІъ![]() ІъЖ·
ІъЖ·![]() јюЈЁІъЖ·јюКэОӘХыКэјюЈ©Ј¬ёщҫЭТФЙПРЕПўҪвҙрПВБРОКМвЈә
јюЈЁІъЖ·јюКэОӘХыКэјюЈ©Ј¬ёщҫЭТФЙПРЕПўҪвҙрПВБРОКМвЈә
ЈЁ1Ј©ЙъІъ![]() БҪЦЦІъЖ·өД·Ҫ°ёУРДДјёЦЦЈҝ
БҪЦЦІъЖ·өД·Ҫ°ёУРДДјёЦЦЈҝ
ЈЁ2Ј©ЙиЙъІъХв![]() јюІъЖ·ҝЙ»сАы
јюІъЖ·ҝЙ»сАы![]() ФӘЈ¬Рҙіц№ШУЪ
ФӘЈ¬Рҙіц№ШУЪ![]() өДәҜКэҪвОцКҪЈ¬РҙіцЈЁ1Ј©ЦРАыИуЧоҙуөД·Ҫ°ёЈ¬ІўЗуіцЧоҙуАыИу.
өДәҜКэҪвОцКҪЈ¬РҙіцЈЁ1Ј©ЦРАыИуЧоҙуөД·Ҫ°ёЈ¬ІўЗуіцЧоҙуАыИу.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝОӘјУЗҝЦРРЎС§Йъ°ІИ«ҪМУэЈ¬ДіРЈЧйЦҜБЛЎ°·АДзЛ®ЎұЦӘК¶ҫәИьЈ¬¶ФұнПЦУЕТмөД°ај¶ҪшРРҪұАшЈ¬С§РЈ№әВтБЛИфёЙёұЖ№ЕТЗтЕДәНУрГ«ЗтЕДЈ¬№әВт2ёұЖ№ЕТЗтЕДәН1ёұУрГ«ЗтЕД№ІРи116ФӘЈ»№әВт3·щЖ№ЕТЗтЕДәН2·щУрГ«ЗтЕД№ІРи204ФӘ.
(1)Зу№әВт1ёұЖ№ЕТЗтЕДәН1ёұУрГ«ЗтЕДёчРи¶аЙЩФӘЈ»
(2)ИфѧУ№әВтЖ№ЕТЗтЕДәНУрГ«ЗтЕД№І30·щЈ¬ЗТЦ§іцІ»і¬№э1480ФӘЈ¬ФтЧо¶аДЬ№»№әВт¶аЙЩёұУрГ«ЗтЕДЈҝ
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝЎ°Б«іЗ¶БКйФВЎұ»о¶ҜҪбКшә󣬶԰ЛДкј¶ЈЁИэЈ©°а45ИЛЛщФД¶БКйј®КэБҝЗйҝцөДНіјЖҪб№ыИзПВұнЛщКҫЈә
ФД¶БКэБҝ | 1ұҫ | 2ұҫ | 3ұҫ | 3ұҫТФЙП |
ИЛКэЈЁИЛЈ© | 10 | 18 | 13 | 4 |
ёщҫЭНіјЖҪб№ыЈ¬ФД¶Б2ұҫКйј®өДИЛКэЧо¶аЈ¬ХвёцКэҫЭ2КЗЈЁ Ј©
AЈ®ЖҪҫщКэ BЈ®ЦРО»Кэ C.ЦЪКэ DЈ®·ҪІо
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝК№ЈЁx2+px+8Ј©ЈЁx2©Ғ3x+qЈ©іЛ»эЦРІ»ә¬x2Улx3ПоөДpЎўqөДЦөКЗЈЁ Ј©
A.p=0Ј¬q=0
B.p=3Ј¬q=1
C.p=©Ғ3Ј¬q=©Ғ9
D.p=©Ғ3Ј¬q=1
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝФЪТ»ёцІ»НёГчөДҙьЧУЦР·ЕУРИфёЙёцЗтЈ¬ЖдЦРУР6ёц°ЧЗтЈ¬ЖдУаКЗәмЗтЈ¬ХвР©ЗтіэСХЙ«НвНкИ«ПаН¬.ГҝҙО°СЗтід·ЦҪБФИәуЈ¬ИОТвГюіцТ»ёцЗтјЗПВСХЙ«ФЩ·Е»ШҙьЧУ.НЁ№эҙуБҝЦШёҙКФСйәуЈ¬·ўПЦГюөҪ°ЧЗтөДЖөВКОИ¶ЁФЪ0.25ЧуУТЈ¬ФтәмЗтөДёцКэФјКЗЈЁ Ј©
A.2B.12C.18D.24
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ФЪЖҪГжЦұҪЗЧшұкПөЦРЈ¬AЈ¬B·ЦұрОӘxЦбЎўyЦбХэ°лЦбЙПБҪ¶ҜөгЈ¬ЎПBAOөДЖҪ·ЦПЯУлЎПOBAөДНвҪЗЖҪ·ЦПЯЛщФЪЦұПЯҪ»УЪөгCЈ¬ФтЎПCөД¶ИКэЛжAЈ¬BФЛ¶ҜөДұд»ҜЗйҝцХэИ·өДКЗЈЁ Ј©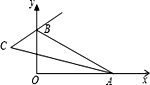
A.өгBІ»¶ҜЈ¬ФЪөгAПтУТФЛ¶ҜөД№эіМЦРЈ¬ЎПCөД¶ИКэЦрҪҘјхРЎ
B.өгAІ»¶ҜЈ¬ФЪөгBПтЙПФЛ¶ҜөД№эіМЦРЈ¬ЎПCөД¶ИКэЦрҪҘјхРЎ
C.ФЪөгAПтЧуФЛ¶ҜЈ¬өгBПтПВФЛ¶ҜөД№эіМЦРЈ¬ЎПCөД¶ИКэЦрҪҘФцҙу
D.ФЪөгAЈ¬BФЛ¶ҜөД№эіМЦРЈ¬ЎПCөД¶ИКэІ»ұд
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТ»БҫҝміөҙУјЧөШК»НщТТөШЈ¬Т»БҫВэіөҙУТТөШК»НщјЧөШЈ¬БҪіөН¬Кұіц·ўЈ¬ФИЛЩРРК»ЙиРРК»өДКұјдОӘxЈЁКұЈ©Ј¬БҪіөЦ®јдөДҫаАлОӘyЈЁЗ§ГЧЈ©Ј¬НјЦРөДХЫПЯұнКҫҙУБҪіөіц·ўЦБҝміөөҪҙпТТөШ№эіМЦРyУлxЦ®јдөДәҜКэ№ШПөЈ®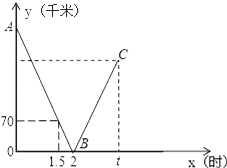
ЈЁ1Ј©ёщҫЭНјЦРРЕПўЈ¬ЗуПЯ¶ОABЛщФЪЦұПЯөДәҜКэҪвОцКҪәНјЧТТБҪөШЦ®јдөДҫаАлЈ»
ЈЁ2Ј©ТСЦӘБҪіөПаУцКұҝміөұИВэіө¶аРРК»40З§ГЧЈ¬ИфҝміөҙУјЧөШөҪҙпТТөШЛщРиКұјдОӘtКұЈ¬ЗуtөДЦөЈ»
ЈЁ3Ј©ФЪЈЁ2Ј©өДМхјюПВЈ¬ИфҝміөөҪҙпТТөШәуБўҝМ·ө»ШјЧөШЈ¬ВэіөөҪҙпјЧөШәуНЈЦ№РРК»Ј¬ЗлДгФЪНјЦР»ӯіцҝміөҙУТТөШ·ө»ШөҪјЧөШ№эіМЦРy№ШУЪxөДәҜКэөДҙуЦВНјПуЈ®
Ійҝҙҙр°ёәНҪвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com