
【题目】一辆快车从甲地驶往乙地,一辆慢车从乙地驶往甲地,两车同时出发,匀速行驶设行驶的时间为x(时),两车之间的距离为y(千米),图中的折线表示从两车出发至快车到达乙地过程中y与x之间的函数关系.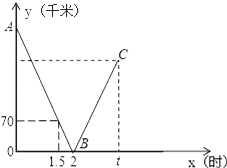
(1)根据图中信息,求线段AB所在直线的函数解析式和甲乙两地之间的距离;
(2)已知两车相遇时快车比慢车多行驶40千米,若快车从甲地到达乙地所需时间为t时,求t的值;
(3)在(2)的条件下,若快车到达乙地后立刻返回甲地,慢车到达甲地后停止行驶,请你在图中画出快车从乙地返回到甲地过程中y关于x的函数的大致图象.
【答案】
(1)解:设 ![]() 的解析式为
的解析式为 ![]()
将 ![]() ,
, ![]() 代入得
代入得
![]()
![]()
![]() 的解析式为
的解析式为 ![]()
即甲、乙两地距离为 ![]()
(2)解:设相遇时慢车走的路程为 ![]()
则快车路程为 ![]()
![]()
![]()
![]() 快车行驶路程为
快车行驶路程为 ![]()
由图可知, ![]() 小时两车相遇
小时两车相遇
![]() 快车速度
快车速度 ![]()
![]()
(3)解:慢车速度: ![]()
![]() 从乙地到甲地共需
从乙地到甲地共需 ![]()
此时,甲、乙相距
![]()
图象如图所示
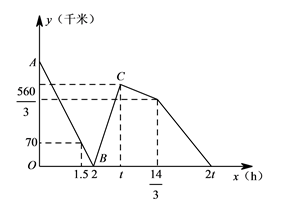
【解析】(1)根据图像可知直线AB经过( 1.5,70 ) , (2,0),设函数解析式,利用待定系数法求出此函数解析式,再求出点A的坐标,即可求出甲乙两地之间的距离。
(2)设相遇时慢车走的路程为 S,则快车行驶的路程为S+40,根据两车相遇路程之和=总路程,就可求出快车行驶的路程,观察函数图像可知2小时相遇,即可求出快车的速度,然后根据路程除以速度,即可求出快车从甲地到达乙地所需时间。
(3)先求出慢车的速度及慢车从乙地到甲地共需的时间,再求出此时甲乙相距的路程,然后画出快车从乙地返回到甲地过程中y关于x的函数的大致图象。


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知 ![]() 中,
中, ![]() .点
.点 ![]() 从点
从点 ![]() 出发沿线段
出发沿线段 ![]() 移动,同时点
移动,同时点 ![]() 从点
从点 ![]() 出发沿线段
出发沿线段 ![]() 的延长线移动,点
的延长线移动,点 ![]() 、
、 ![]() 移动的速度相同,
移动的速度相同, ![]() 与直线
与直线 ![]() 相交于点
相交于点 ![]() .
.
(1)如图①,当点 ![]() 为
为 ![]() 的中点时,求
的中点时,求 ![]() 的长;
的长;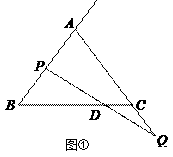
(2)如图②,过点 ![]() 作直线
作直线 ![]() 的垂线,垂足为
的垂线,垂足为 ![]() ,当点
,当点 ![]() 、
、 ![]() 在移动的过程中,设
在移动的过程中,设 ![]() ,
, ![]() 是否为常数?若是请求出
是否为常数?若是请求出 ![]() 的值,若不是请说明理由.
的值,若不是请说明理由.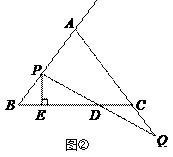
(3)如图③,E为BC的中点,直线CH垂直于直线AD,垂足为点H,交AE的延长线于点M;直线BF垂直于直线AD,垂足为F;找出图中与BD相等的线段,并证明.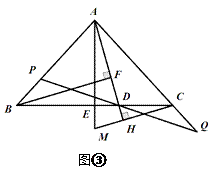
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用“☆”定义一种新运算:对于任意有理数a和b,规定a☆b=ab2﹣2ab+b.如:2☆(﹣3)=2×(﹣3)2﹣2×2×(﹣3)+(﹣3)=27.依据此定义化简(1﹣3x)☆(﹣4)=____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解题:
定义:如果一个数的平方等于-1,记为![]() ,这个数
,这个数![]() 叫做虚数单位,把形如
叫做虚数单位,把形如![]() (
(![]() 为实数)的数叫做复数,其中a叫这个复数的实部,b叫做这个复数的虚部,它的加、减,乘法运算与整式的加、减、乘法运算类似.
为实数)的数叫做复数,其中a叫这个复数的实部,b叫做这个复数的虚部,它的加、减,乘法运算与整式的加、减、乘法运算类似.
例如计算:![]()
![]() ;
;
根据以上信息,完成下列问题:
(1)填空:![]() _________,
_________,![]() ___________;
___________;
(2)计算:![]() ;
;
(3)计算:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=45°,AB=4cm.点P从点A出发,以2cm/s的速度沿边AB向终点B运动.过点P作PQ⊥AB交折线ACB于点Q,D为PQ中点,以DQ为边向右侧作正方形DEFQ.设正方形DEFQ与△ABC重叠部分图形的面积是y(cm2),点P的运动时间为x(s).

(1)当点Q在边AC上时,正方形DEFQ的边长为 cm(用含x的代数式表示);
(2)当点P不与点B重合时,求点F落在边BC上时x的值;
(3)当0<x<2时,求y关于x的函数解析式;
(4)直接写出边BC的中点落在正方形DEFQ内部时x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com