
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=45°,AB=4cm.点P从点A出发,以2cm/s的速度沿边AB向终点B运动.过点P作PQ⊥AB交折线ACB于点Q,D为PQ中点,以DQ为边向右侧作正方形DEFQ.设正方形DEFQ与△ABC重叠部分图形的面积是y(cm2),点P的运动时间为x(s).

(1)当点Q在边AC上时,正方形DEFQ的边长为 cm(用含x的代数式表示);
(2)当点P不与点B重合时,求点F落在边BC上时x的值;
(3)当0<x<2时,求y关于x的函数解析式;
(4)直接写出边BC的中点落在正方形DEFQ内部时x的取值范围.
【答案】(1)x;(2)x=![]() ;(3)见解析;(4)1<x<
;(3)见解析;(4)1<x<![]() .
.
【解析】
试题分析:(1)由已知条件得到∠AQP=45°,求得PQ=AP=2x,由于D为PQ中点,于是得到DQ=x;
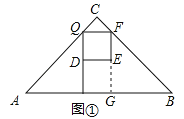
(2)如图①,延长FE交AB于G,由题意得AP=2x,由于D为PQ中点,得到DQ=x,求得GP=2x,列方程于是得到结论;
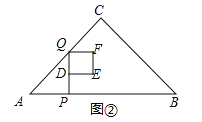
(3)如图②,当0<x≤![]() 时,根据正方形的面积公式得到y=x2;如图③,当
时,根据正方形的面积公式得到y=x2;如图③,当![]() <x≤1时,过C作CH⊥AB于H,交FQ于K,则CH=
<x≤1时,过C作CH⊥AB于H,交FQ于K,则CH=![]() AB=2,根据正方形和三角形面积公式得到y=﹣
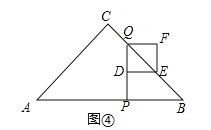
AB=2,根据正方形和三角形面积公式得到y=﹣![]() x2+20x﹣8;如图④,当1<x<2时,PQ=4﹣2x,根据三角形的面积公式得到结论;
x2+20x﹣8;如图④,当1<x<2时,PQ=4﹣2x,根据三角形的面积公式得到结论;
(4)当Q与C重合时,E为BC的中点,得到x=1,当Q为BC的中点时,BQ=![]() ,得到x=
,得到x=![]() ,于是得到结论.
,于是得到结论.
试题解析:(1)∵∠ACB=90°,∠A=45°,PQ⊥AB,
∴∠AQP=45°,
∴PQ=AP=2x,
∵D为PQ中点,
∴DQ=x,
(2)如图①,延长FE交AB于G,由题意得AP=2x,
∵D为PQ中点,
∴DQ=x,
∴GP=2x,
∴2x+x+2x=4,
∴x=![]() ;
;
(3)如图②,当0<x≤![]() 时,y=S正方形DEFQ=DQ2=x2,
时,y=S正方形DEFQ=DQ2=x2,
∴y=x2;
如图③,当![]() <x≤1时,过C作CH⊥AB于H,交FQ于K,则CH=
<x≤1时,过C作CH⊥AB于H,交FQ于K,则CH=![]() AB=2,
AB=2,

∵PQ=AP=2x,CK=2﹣2x,
∴MQ=2CK=4﹣4x,FM=x﹣(4﹣4x)=5x﹣4,
∴y=S正方形DEFQ﹣S△MNF=DQ2﹣![]() FM2,
FM2,
∴y=x2﹣![]() (5x﹣4)2=﹣
(5x﹣4)2=﹣![]() x2+20x﹣8,
x2+20x﹣8,
∴y=﹣![]() x2+20x﹣8;
x2+20x﹣8;
如图④,当1<x<2时,PQ=4﹣2x,
∴DQ=2﹣x,
∴y=S△DEQ=![]() DQ2,
DQ2,
∴y=![]() (2﹣x)2,
(2﹣x)2,
∴y=![]() x2﹣2x+2;
x2﹣2x+2;
(4)当Q与C重合时,E为BC的中点,
即2x=2,
∴x=1,
当Q为BC的中点时,BQ=![]() ,
,
PB=1,
∴AP=3,
∴2x=3,
∴x=![]() ,
,
∴边BC的中点落在正方形DEFQ内部时x的取值范围为:1<x<![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A,B分别为x轴、y轴正半轴上两动点,∠BAO的平分线与∠OBA的外角平分线所在直线交于点C,则∠C的度数随A,B运动的变化情况正确的是( )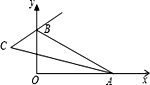
A.点B不动,在点A向右运动的过程中,∠C的度数逐渐减小
B.点A不动,在点B向上运动的过程中,∠C的度数逐渐减小
C.在点A向左运动,点B向下运动的过程中,∠C的度数逐渐增大
D.在点A,B运动的过程中,∠C的度数不变
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆快车从甲地驶往乙地,一辆慢车从乙地驶往甲地,两车同时出发,匀速行驶设行驶的时间为x(时),两车之间的距离为y(千米),图中的折线表示从两车出发至快车到达乙地过程中y与x之间的函数关系.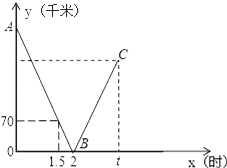
(1)根据图中信息,求线段AB所在直线的函数解析式和甲乙两地之间的距离;
(2)已知两车相遇时快车比慢车多行驶40千米,若快车从甲地到达乙地所需时间为t时,求t的值;
(3)在(2)的条件下,若快车到达乙地后立刻返回甲地,慢车到达甲地后停止行驶,请你在图中画出快车从乙地返回到甲地过程中y关于x的函数的大致图象.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】利用二元一次方程组解应用题:甲、乙两地相距 ![]() ,一辆汽车和一辆拖拉机同时由两地以各自的速度匀速相向而行,
,一辆汽车和一辆拖拉机同时由两地以各自的速度匀速相向而行, ![]() 小时后相遇.相遇后,拖拉机以其原速继续前进,汽车在相遇处停留
小时后相遇.相遇后,拖拉机以其原速继续前进,汽车在相遇处停留 ![]() 小时后调转车头以其原速返回,在汽车再次出发半小时追上拖拉机.这时,汽车、拖拉机各自走了多少路程?
小时后调转车头以其原速返回,在汽车再次出发半小时追上拖拉机.这时,汽车、拖拉机各自走了多少路程?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法不正确的是( )
A.“某射击运动员射击一次,正中靶心”属于随机事件
B.“13名同学至少有两名同学的出生月份是相同的”属于必然事件
C.“在标准大气压下,当温度降到-5℃时,水结成冰”属于随机事件
D.“某袋中有8个质地均匀的球,且都是红球,任意摸出一球是白球”属于不可能事件
查看答案和解析>>
科目:初中数学 来源: 题型:
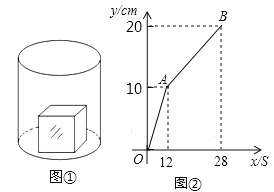
【题目】如图①,一个正方体铁块放置在圆柱形水槽内,现以一定的速度往水槽中注水,28s时注满水槽.水槽内水面的高度y(cm)与注水时间x(s)之间的函数图象如图②所示.
(1)正方体的棱长为 cm;
(2)求线段AB对应的函数解析式,并写出自变量x的取值范围;
(3)如果将正方体铁块取出,又经过t(s)恰好将此水槽注满,直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】初一(1)班针对“你最喜爱的课外活动项目”对全班学生进行调查(每名学生分别选一个活动项目),并根据调查结果列出统计表,绘制成扇形统计图.

根据以上信息解决下列问题:
(1)![]() ,
,![]() ;
;
(2)扇形统计图中机器人项目所对应扇形的圆心角度数为 ![]() ;
;
(3)从选航模项目的![]() 名学生中随机选取
名学生中随机选取![]() 名学生参加学校航模兴趣小组训练,请用列举法(画树状图或列表)求所选取的
名学生参加学校航模兴趣小组训练,请用列举法(画树状图或列表)求所选取的![]() 名学生中恰好有
名学生中恰好有![]() 名男生、
名男生、![]() 名女生的概率.
名女生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com