
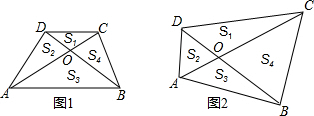
���� ��1���ɡ�ABO�ס�CDO�ɵó����Ʊȣ������ó����������ε�����ȣ����ɵȻ��任��֤��S2=S4���Ӷ�����Ȼ�ó���
��2��ע�$\frac{{S}_{1}}{{S}_{2}}=\frac{CO}{AO}=\frac{{S}_{4}}{{S}_{3}}$�����۲��Զ�����
��3��֤��ͬ��2����
��� �⣺��1����AB��CD��
���ABO�ס�CDO��
��$\frac{AB}{CD}=\frac{AO}{CO}=\frac{BO}{DO}=2$��
��$\frac{{S}_{1}}{{S}_{3}}=��\frac{CD}{AB}��^{2}$=$\frac{1}{4}$��
��$\frac{{S}_{1}}{{S}_{2}}=\frac{CO}{AO}=\frac{1}{2}$��
��S1��S2��S3=1��2��4��
��S1+S2=S1+S4��
��S2=S4��
��S1��S2��S3��S4=1��2��4��2��
�ʴ�Ϊ1��2��4��2��
��2����$\frac{{S}_{1}}{{S}_{2}}=\frac{CO}{AO}=\frac{{S}_{4}}{{S}_{3}}$��
��S1•S3=S2•S4��
�ʴ�ΪS1•S3=S2•S4��
��3����Ȼ������
��$\frac{{S}_{1}}{{S}_{2}}=\frac{CO}{AO}=\frac{{S}_{4}}{{S}_{3}}$��
��S1•S3=S2•S4��
���� ���⿼�������������ε��ж������ʡ��Ȼ��任���ѶȲ�����ʵ�ϣ�������֤��������Сѧ�������ģ�͵��еĺ�����������ס�˽��۶��ڽ����ص���������кܴ�İ�����


 ÿ��10���ӿ�����������������ϵ�д�
ÿ��10���ӿ�����������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
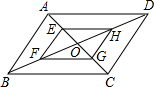 ��ͼ����?ABCD�У��Խ���AC��BD�ཻ�ڵ�O����G��F��G��H���ֱ���AO��BO��CO��DO�ϵĵ㣮
��ͼ����?ABCD�У��Խ���AC��BD�ཻ�ڵ�O����G��F��G��H���ֱ���AO��BO��CO��DO�ϵĵ㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com