
如图,小敏做了一个角平分仪ABCD,其中AB=AD,BC=DC.将仪器上的点 A与∠PRQ的顶点R重合,调整AB和AD,使它们分别落在角的两边上,过点A,C画一条射线AE,AE就是∠PRQ的平分线.此角平分仪的画图原理是:根据仪器结构,可得
A与∠PRQ的顶点R重合,调整AB和AD,使它们分别落在角的两边上,过点A,C画一条射线AE,AE就是∠PRQ的平分线.此角平分仪的画图原理是:根据仪器结构,可得
△ABC≌△ADC,这样就有∠QAE=∠PAE.则说明这两个三角形全等的依据是( )

A.SAS B.ASA C.AAS D.SSS
科目:初中数学 来源: 题型:
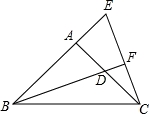
.如图,在△ABC中,∠BAC=90°,AB=AC,D在AC上,过C作CE⊥BD的延长线于F,交BA的延长线于E.
(1)BD与CE相等吗?请说明理由;
(2)BE与AC+AD相等吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,由四个小正方形组成的田字格中,△ABC的顶点都是小正方形的顶点.在田字格上画与△ABC成轴对称的三角形,且顶点都是小正方形的顶点,则这样的三角形(不包含△ABC本身)共有( )
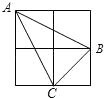
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
观察下列勾股数:
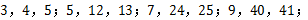 …
… 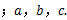
根据你发现的规律,解答下列问题:
(1)当 时,求
时,求 的值;
的值;
(2)当 时,求
时,求 的值;
的值;
(3)用(2)的结论判断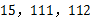 是否为一组勾股数,并说明理由.
是否为一组勾股数,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com