
【题目】在四边形ABCD中,对角线AC、BD相交于点O,设锐角∠AOB=α,将△DOC按逆时针方向旋转得到△D′OC′(0°<旋转角<90°)连接AC′、BD′,AC′与BD′相交于点M.

(1)、当四边形ABCD为矩形时,如图1.求证:△AOC′≌△BOD′.
(2)、当四边形ABCD为平行四边形时,设AC=kBD,如图2.
①猜想此时△AOC′与△BOD′有何关系,证明你的猜想;
②探究AC′与BD′的数量关系以及∠AMB与α的大小关系,并给予证明.
【答案】(1)、证明过程见解析;(2)、①、△BOD′∽△AOC′,证明过程见解析;(2)、AC′=kBD′,∠AMB=α,证明过程见解析.
【解析】
试题分析:(1)、根据矩形的性质得出OA=OC=OB=OD,根据旋转可得OD=OD′,OC=OC′,∠D′OD=∠C′OC,根据平角得出∠BOD′=∠AOC′,从而说明三角形全等;(2)、根据平行四边形的性质得出OB=OD,OA=OC,根据旋转得出OD=OD′,OC=OC′,∠D′OD=∠C′OC,根据平角的性质得出∠BOD′=∠AOC′,从而得出三角形相似;根据三角形相似的性质进行说明.
试题解析:(1)、在矩形ABCD中,∵AC=BD,OA=OC=![]() AC,OB=OD=
AC,OB=OD=![]() BD,
BD,
∴OA=OC=OB=OD,∵△D′OC′由△DOC旋转得到,∴OD=OD′,OC=OC′,∠D′OD=∠C′OC,
∴OB=OD′=OA=OC′,∴180°-∠D′OD=180°-∠C′OC, 即∠BOD′=∠AOC′,
∴△BOD′≌△AOC′
(2)、①猜想:△BOD′∽△AOC′.
∵在平行四边形ABCD中,OB=OD,OA=OC, ∵△D′OC′由△DOC旋转得到,
∴OD=OD′,OC=OC′,∠D′OD=∠C′OC, ∴OB:OA=OD′:OC′,180°-∠D′OD=180°-∠C′OC,
∴∠BOD′=∠AOC′, ∴△BOD′∽△AOC′
②结论:AC′=kBD′,∠AMB=α
∵△BOD′∽△AOC′, ∴![]() ,即AC′=kBD′
,即AC′=kBD′
设BD′与AC相交于点N,∵△BOD′∽△AOC′,∴∠OBM=∠OAM,
在△ANM与△BNO中,又∵∠ANM=∠BNO,
∴180°-∠OAC′-∠ANM=180°-∠OBD′-∠BNO,
即∠AMB=∠AOB=α.


科目:初中数学 来源: 题型:
【题目】已知样本数据x1 , x2 , x3 , …,xn的方差为4,则数据2x1+3,2x2+3,2x3+3,…,2xn+3的方差为( )
A.11
B.9
C.16
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:EF∥AD,∠1=∠2,∠BAC=75°.将求∠AGD的过程填写完整.
 解:∵EF∥AD (已知)
解:∵EF∥AD (已知)
∴∠2= ( )
又∵∠1=∠2 (已知)∴∠1=∠3( )
∴AB∥ ( )
∴∠BAC+ =180°( )
∵∠BAC=75°(已知)
∴∠AGD= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】⊙O的半径为5cm,点A到圆心O的距离OA=3cm,则点A与圆O的位置关系为( )
A.点A在圆上 B.点A在圆内 C.点A在圆外 D.无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,点P在BA的延长线上,PD切⊙O于点D,过点B作BE垂直于PD,交PD的延长线于点C,连接AD并延长,交BE于点E。

(1)求证:AB=BE;
(2)若PA=2 ,cosB=![]() ,求⊙O半径的长。
,求⊙O半径的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解某县七年级9800名学生的视力情况,从中抽查了100名学生的视力情况,就这个问题来说,下面说法正确的是( )
A. 9800名学生是总体 B. 每个学生是个体
C. 100名学生是所抽取的一个样本 D. 样本容量是100
查看答案和解析>>
科目:初中数学 来源: 题型:
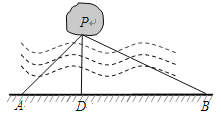
【题目】如图,湖中有一小岛,湖边有一条笔直的观光小道AB,现决定从小岛架一座与观光小道垂直的小桥PD,在小道上测得如下数据:AB=60米,∠PAB=45°,∠PBA=30°.请求出小桥PD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com