
分析 (1)根据分式乘法的法则,将分子、分母约分相乘即可;
(2)根据分式除法的法则,将除法转化为乘法,约分相乘即可;
(3)根据分式乘法的法则,将分子、分母分解因式,约分相乘即可;
(4)根据分式除法的法则,将除法转化为乘法;将分子、分母分解因式,约分相乘即可.
解答 解:(1)$\frac{{n}^{2}}{2m}•\frac{4{m}^{2}}{5{n}^{3}}=\frac{2m}{5n}$;
(2)原式=$\frac{5{b}^{2}}{3ac}×(-\frac{21a}{10bc})=-\frac{7b}{2{c}^{2}}$;
(3)原式=$\frac{x+2}{x-3}•\frac{(x-3)^{2}}{(x+2)(x-2)}=\frac{x+3}{x-2}$;
(4)原式=$\frac{(a+1)(a-1)}{(a+1)^{2}}•\frac{a+1}{a(a-1)}=\frac{1}{a}$.
点评 本题主要考查分式的乘除法.熟记分式的乘除法法则且能够熟练将多项式因式分解是解决此题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
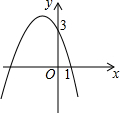 已知二次函数y=ax2+bx+c的图象如图所示,则函数关系式是( )
已知二次函数y=ax2+bx+c的图象如图所示,则函数关系式是( )| A. | y=x2-2x+3 | B. | y=-x2-2x+3 | C. | y=x2+2x+3 | D. | y=-x2+2x+3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 掷一枚均匀的骰子,骰子停止运动后,6点朝上是必然事件 | |
| B. | 太阳从西边升起是不可能事件 | |
| C. | “明天降雨的概率为$\frac{1}{2}$”,表示明天有半天都在降雨 | |
| D. | 一个游戏中奖的概率是$\frac{1}{100}$,则做100次这样的游戏一定会中奖 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com