
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交BC,AC于点D,E,DG⊥AC于点G,交AB的延长线于点F.
(1)求证:直线FG是⊙O的切线;
(2)若AC=10,cosA=![]() ,求CG的长.
,求CG的长.
【答案】
(1)
证明:如图1,连接OD,

∵AB=AC,
∴∠C=∠ABC,
∵OD=OB,
∴∠ABC=∠ODB,
∴∠ODB=∠C,
∴OD∥AC,
∴∠ODG=∠DGC,
∵DG⊥AC,
∴∠DGC=90°,
∴∠ODG=90°,
∴OD⊥FG,
∵OD是⊙O的半径,
∴直线FG是⊙O的切线.
(2)
解:如图2,
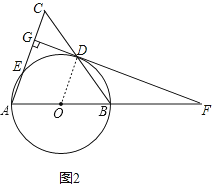
∵AB=AC=10,AB是⊙O的直径,
∴OA=OD=10÷2=5,
由(1),可得
OD⊥FG,OD∥AC,
∴∠ODF=90°,∠DOF=∠A,
在△ODF和△AGF中,
![]()
∴△ODF∽△AGF,
∴![]() ,
,
∵cosA=![]() ,
,
∴cos∠DOF=![]() ,
,
∴![]() =
=![]() =
=![]() ,
,
∴AF=AO+OF=5![]() ,
,
∴![]() ,
,
解得AG=7,
∴CG=AC﹣AG=10﹣7=3,
即CG的长是3.
【解析】(1)首先判断出OD∥AC,推得∠ODG=∠DGC,然后根据DG⊥AC,可得∠DGC=90°,∠ODG=90°,推得OD⊥FG,即可判断出直线FG是⊙O的切线.
(2)首先根据相似三角形判定的方法,判断出△ODF∽△AGF,再根据cosA=![]() ,可得cos∠DOF=
,可得cos∠DOF=![]() ;然后求出OF、AF的值,即可求出AG、CG的值各是多少.
;然后求出OF、AF的值,即可求出AG、CG的值各是多少.
【考点精析】认真审题,首先需要了解切线的判定定理(切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线),还要掌握相似三角形的判定与性质(相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方)的相关知识才是答题的关键.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:
【题目】我国是世界上严重缺水的国家之一,全国总用水量逐年上升,全国总用水量可分为农业用水量、工业用水量和生活用水量三部分.为了合理利用水资源,我国连续多年对水资源的利用情况进行跟踪调查,将所得数据进行处理,绘制了2008年全国总用水量分布情况扇形统计图和2004﹣2008年全国生活用水量折线统计图的一部分如下(A指农业用水量;B指工业用水量;C指生活用水量):
(1)2007年全国生活用水量比2004年增加了16%,则2004年全国生活用水量为____亿m3 , 2008年全国生活用水量比2004年增加了20%,则2008年全国生活用水量为____亿m3;
(2)根据以上信息,请直接在答题卡上补全折线统计图;
(3)根据以上信息2008年全国总水量为___亿m3;
(4)我国2008年水资源总量约为2.75×104亿m3 , 根据国外的经验,一个国家当年的全国总用水量超过这个国家年水资源总量的20%,就有可能发生“水危机”.依据这个标准,2008年我国是否属于可能发生“水危机”的行列?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,小明家小区空地上有两颗笔直的树CD、EF.一天,他在A处测得树顶D的仰角∠DAC=30°,在B处测得树顶F的仰角∠FBE=45°,线段BF恰好经过树顶D.已知A、B两处的距离为2米,两棵树之间的距离CE=3米,A、B、C、E四点在一条直线上,求树EF的高度.(![]() ≈1.7,
≈1.7,![]() ≈1.4,结果保留一位小数)
≈1.4,结果保留一位小数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OABC,OA=3,OC=6,将△ABC沿对角线AC翻折,使点B落在点B′处,AB′与y轴交于点D,则点D的坐标为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种电缆在空中架设时,两端挂起的电缆下垂都近似抛物线y= ![]() x2的形状.今在一个坡度为1:5的斜坡上,沿水平距离间隔50米架设两固定电缆的位置离地面高度为20米的塔柱(如图),这种情况下在竖直方向上,下垂的电缆与地面的最近距离为( )
x2的形状.今在一个坡度为1:5的斜坡上,沿水平距离间隔50米架设两固定电缆的位置离地面高度为20米的塔柱(如图),这种情况下在竖直方向上,下垂的电缆与地面的最近距离为( ) 
A.12.75米
B.13.75米
C.14.75米
D.17.75米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某人在山坡坡脚A处测得电视塔尖点C的仰角为60°,沿山坡向上走到P处再测得点C的仰角为45°,已知OA=100米,山坡坡度(竖直高度与水平宽度的比)i=1:2,且O、A、B在同一条直线上.求电视塔OC的高度以及此人所在位置点P的铅直高度.(测倾器高度忽略不计,结果保留根号形式)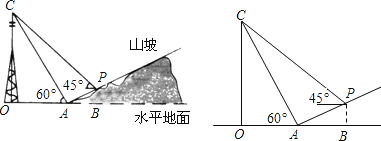
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地区共有1800名初三学生,为了解这些学生的体质健康状况,开学之初随机选取部分学生进行体育测试,以下是根据测试成绩绘制的统计图表的一部分.
等级 | 测试成绩(分) | 人数 |
优秀 | 45≤x≤50 | 140 |
良好 | 37.5≤x<45 | 36 |
及格 | 30≤x<37.5 | |
不及格 | x<30 | 6 |

根据以上信息,解答下列问题:
(1)本次测试学生体质健康成绩为良好的有人,达到优秀的人数占本次测试总人数的百分比为%.
(2)本次测试的学生数为人,其中,体质健康成绩为及格的有人,不及格的人数占本次测试总人数的百分比为%.
(3)试估计该地区初三学生开学之初体质健康成绩达到良好及以上等级的学生数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com