
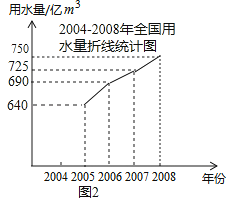
【题目】我国是世界上严重缺水的国家之一,全国总用水量逐年上升,全国总用水量可分为农业用水量、工业用水量和生活用水量三部分.为了合理利用水资源,我国连续多年对水资源的利用情况进行跟踪调查,将所得数据进行处理,绘制了2008年全国总用水量分布情况扇形统计图和2004﹣2008年全国生活用水量折线统计图的一部分如下(A指农业用水量;B指工业用水量;C指生活用水量):
(1)2007年全国生活用水量比2004年增加了16%,则2004年全国生活用水量为____亿m3 , 2008年全国生活用水量比2004年增加了20%,则2008年全国生活用水量为____亿m3;
(2)根据以上信息,请直接在答题卡上补全折线统计图;
(3)根据以上信息2008年全国总水量为___亿m3;
(4)我国2008年水资源总量约为2.75×104亿m3 , 根据国外的经验,一个国家当年的全国总用水量超过这个国家年水资源总量的20%,就有可能发生“水危机”.依据这个标准,2008年我国是否属于可能发生“水危机”的行列?并说明理由.
【答案】
(1)
解:设2004年全国生活用水量为x亿m3,
根据题意得x(1+16%)=725,解得x=625,
即2004年全国生活用水量为625亿m3,
则2008年全国生活用水量=625×(1+20%)=750(亿m3);
故答案为:625,750.
(2)
解:如图:
(3)
解:2008年全国总水量=750÷15%=5000(亿m3);
故答案为:5000.
(4)
解:不属于.理由如下:
2.75×104×20%=5500>5000,
所以2008年我国不属于可能发生“水危机”的行列.
【解析】(1)设2004年全国生活用水量为x亿m3 , 利用增长率公式得到x(1+16%)=725,解得x=625,然后计算用(1+20%)乘以2004的全国生活用水量得到2008年全国生活用水量;
(2)补全折线统计图即可;
(3)用2008年全国生活用水量除以2008年全国生活用水量所占的百分比即可得到2008年全国总水量;
(4)通过计算得到2.75×104×20%=5500>5000,根据题意可判断2008年我国不属于可能发生“水危机”的行列.
【考点精析】关于本题考查的扇形统计图和折线统计图,需要了解能清楚地表示出各部分在总体中所占的百分比.但是不能清楚地表示出每个项目的具体数目以及事物的变化情况;能清楚地反映事物的变化情况,但是不能清楚地表示出在总体中所占的百分比才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,O是坐标原点,ABCD的顶点A的坐标为(﹣2,0),点D的坐标为(0,2 ![]() ),点B在x轴的正半轴上,点E为线段AD的中点,过点E的直线l与x轴交于点F,与射线DC交于点G.
),点B在x轴的正半轴上,点E为线段AD的中点,过点E的直线l与x轴交于点F,与射线DC交于点G.
(1)求∠DCB的度数;
(2)当点F的坐标为(﹣4,0)时,求点G的坐标;
(3)连接OE,以OE所在直线为对称轴,△OEF经轴对称变换后得到△OEF',记直线EF'与射线DC的交点为H.
如图2,当点G在点H的左侧时,求证:△DEG∽△DHE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】云南鲁甸发生地震后,某社区开展献爱心活动,社区党员积极向灾区捐款,如图是该社区部分党员捐款情况的条形统计图,那么本次捐款钱数的众数和中位数分别是( )
A.100元,100元
B.100元,200元
C.200元,100元
D.200元,200元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两车在途中相遇后分别按原速同时驶往甲地,两车之间的距离S(km)与慢车行驶时间t(h)之间的函数图象如图所示,
下列说法:
①甲、乙两地之间的距离为560km;
②快车速度是慢车速度的1.5倍;
③快车到达甲地时,慢车距离甲地60km;
④相遇时,快车距甲地320km
其中正确的个数是( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:点D是等腰直角三角形ABC斜边BC所在直线上一点(不与点B重合),连接AD.
(1)如图1,当点D在线段BC上时,将线段AD绕点A逆时针方向旋转90°得到线段AE,连接CE.求证:BD=CE,BD⊥CE.
(2)如图2,当点D在线段BC延长线上时,探究AD、BD、CD三条线段之间的数量关系,写出结论并说明理由;(3)若BD=![]() CD,直接写出∠BAD的度数.
CD,直接写出∠BAD的度数.
(3)若BD=![]() CD,直接写出∠BAD的度数.
CD,直接写出∠BAD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AB=6,BC=4,∠B=60°,点E是边AB上的一点,点F是边CD上一点,将ABCD沿EF折叠,得到四边形EFGH,点A的对应点为点H,点D的对应点为点G.
(1)当点H与点C重合时.
①填空:点E到CD的距离是___;
②求证:△BCE≌△GCF;
③求△CEF的面积;
(2)当点H落在射线BC上,且CH=1时,直线EH与直线CD交于点M,请直接写出△MEF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AC=BC,斜边AB=2,O是AB的中点,以O为圆心,线段OC的长为半径画圆心角为90°的扇形OEF,弧EF经过点C,则图中阴影部分的面积为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交BC,AC于点D,E,DG⊥AC于点G,交AB的延长线于点F.
(1)求证:直线FG是⊙O的切线;
(2)若AC=10,cosA=![]() ,求CG的长.
,求CG的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com