Question

【题目】如图，在ABCD中，AB=6，BC=4，∠B=60°，点E是边AB上的一点，点F是边CD上一点，将ABCD沿EF折叠，得到四边形EFGH，点A的对应点为点H，点D的对应点为点G．

（1）当点H与点C重合时．
①填空：点E到CD的距离是___；
②求证：△BCE≌△GCF；
③求△CEF的面积；
（2）当点H落在射线BC上，且CH=1时，直线EH与直线CD交于点M，请直接写出△MEF的面积．

Answer 1

【答案】
（1）

解：如图1，

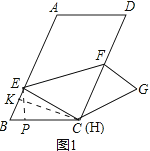
①作CK⊥AB于K，

∵∠B=60°，

∴CK=BCsin60°=4×=2，

∵C到AB的距离和E到CD的距离都是平行线AB、CD间的距离，

∴点E到CD的距离是2，

故答案为2；

②∵四边形ABCD是平行四边形，

∴AD=BC，∠D=∠B，∠A=∠BCD，

由折叠可知，AD=CG，∠D=∠G，∠A=∠ECG，

∴BC=GC，∠B=∠G，∠BCD=∠ECG，

∴∠BCE=∠GCF，

在△BCE和△GCF中，

，

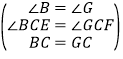∴△BCE≌△GCF（ASA）；

③过E点作EP⊥BC于P，

∵∠B=60°，∠EPB=90°，

∴∠BEP=30°，

∴BE=2BP，

设BP=m，则BE=2m，

∴EP=BEsin60°=2m×=m，

由折叠可知，AE=CE，

∵AB=6，

∴AE=CE=6﹣2m，

∵BC=4，

∴PC=4﹣m，

在Rt△ECP中，由勾股定理得（4﹣m）2+（m）2=（6﹣2m）2，解得m=，

∴EC=6﹣2m=6﹣2×=，

∵△BCE≌△GCF，

∴CF=EC=，

∴S△CEF=××2=；

（2）

解：①当H在BC的延长线上，且位于C点的右侧时时，如图2，过E点作EQ⊥BC于Q，

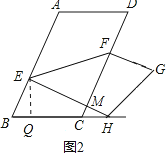
∵∠B=60°，∠EQB=90°，

∴∠BEQ=30°，

∴BE=2BQ，

设BQ=n，则BE=2n，

∴QE=BEsin60°=2n×=n，

由折叠可知，AE=HE，

∵AB=6，

∴AE=HE=6﹣2n，

∵BC=4，CH=1，

∴BH=5，

∴QH=5﹣n，

在Rt△EHQ中，由勾股定理得（5﹣n）2+（n）2=（6﹣2n）2，解得n=，

∴AE=HE=6﹣2n=，

∵AB∥CD，

∴△CMH∽△BEH，

∴=，即=，

∴MH=，

∴EM=﹣=

∴S△EMF=××2=．

②如图3，当H在线段BC上时，过E点作EQ⊥BC于Q，

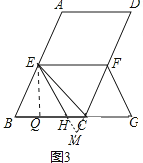
∵∠B=60°，∠EQB=90°，

∴∠BEQ=30°，

∴BE=2BQ，

设BQ=n，则BE=2n，

∴QE=BEsin60°=2n×=n，

由折叠可知，AE=HE，

∵AB=6，

∴AE=HE=6﹣2n，

∵BC=4，CH=1，

∴BH=3

∴QH=3﹣n

在Rt△EHQ中，由勾股定理得（3﹣n）2+（n）2=（6﹣2n）2，解得n=

∴BE=2n=3，AE=HE=6﹣2n=3，

∴BE=BH，

∴∠B=60°，

∴△BHE是等边三角形，

∴∠BEH=60°，

∵∠AEF=∠HEF，

∴∠FEH=∠AEF=60°，

∴EF∥BC，

∴DF=CF=3，

∵AB∥CD，

∴△CMH∽△BEH，

∴=，即=，

∴CM=1

∴EM=CF+CM=4

∴S△EMF=×4×2=4．

综上，△MEF的面积为或4．

【解析】（1）①解直角三角形即可；
②根据平行四边形的性质和折叠的性质得出∠B=∠G，∠BCE=∠GCF，BC=GC，然后根据AAS即可证明；③过E点作EP⊥BC于P，设BP=m，则BE=2m，通过解直角三角形求得EP=m，然后根据折叠的性质和勾股定理求得EC，进而根据三角形的面积就可求得；
（2）过E点作EQ⊥BC于Q，通过解直角三角形求得EP=n，根据折叠的性质和勾股定理求得EH，然后根据三角形相似对应边成比例求得MH，从而求得CM，然后根据三角形面积公式即可求得．
【考点精析】认真审题，首先需要了解平行四边形的性质(平行四边形的对边相等且平行；平行四边形的对角相等，邻角互补；平行四边形的对角线互相平分)，还要掌握翻折变换（折叠问题）(折叠是一种对称变换，它属于轴对称，对称轴是对应点的连线的垂直平分线，折叠前后图形的形状和大小不变，位置变化，对应边和角相等)的相关知识才是答题的关键．