
已知,如图,矩形ABCD中,E是CD的中点,连接BE并延长BE交AD的延长线于点F,连接AE.
(1)求证:AD=DF;
(2)若AD=3,AE⊥BE,求AB的长.


【考点】矩形的性质;全等三角形的判定与性质;勾股定理.
【专题】几何综合题.
【分析】(1)根据E是CD的中点,BC∥AF可确定EF=EB,从而得出△EBC≌△EFD,继而得出结论.
(2)由(1)得出的EF=EB,结合AE⊥BE可得AB=AF,从而根据AD=3可得出答案.
【解答】解:(1)∵BC∥AF,E是CD的中点,
∴E是线段FB的中点,
∴FE=EB,
又∠FED=∠BEC,DE=EC,
∴△EBC≌△EFD,
∴AD=DF.
(2)由(1)得:EF=EB,
又AE⊥BE,
∴AB=AF(中垂线的性质)
∴AB=AF=2AD=6.
【点评】本题考查了矩形的性质及勾股定理的知识,有一定的难度,解答本题的关键是根据题意得出E是FB的中点,这是本题的突破口.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案科目:初中数学 来源: 题型:
如图放置的△OAB1,△B1A1B2,△B2A2B3,…都是边长为1的等边三角形,点A在x轴上,点O,B1,B2,B3,…都在直线l上,则点A2016的坐标是 .


查看答案和解析>>
科目:初中数学 来源: 题型:
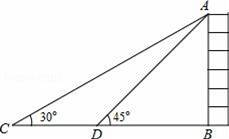
如图,某校数学兴趣小组为测得大厦AB的高度,在大厦前的平地上选择一点C,测得大厦顶端A的仰角为30°,再向大厦方向前进80米,到达点D处(C、D、B三点在同一直线上),又测得大厦顶端A的仰角为45°,请你计算该大厦的高度.(精确到0.1米,参考数据: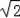
 ≈1.414,
≈1.414,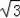
 ≈1.732)
≈1.732)

查看答案和解析>>
科目:初中数学 来源: 题型:
下列命题中,正确的是( )
A.对角线相等的四边形是矩形
B.对角线互相平分的四边形是平行四边形
C.对角线互相垂直的四边形是菱形
D.对角线互相垂直且相等的四边形是正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
已知:直线x-2y=-k+6和x+3y=4k+1,若它们的交点在第四象限内.
(1)求k的取值范围.
(2)若k为非负整数,求直线x-2y=-k+6和x+3y=4k+1分别与y轴的交点,及它们的交点所围成的三角形的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com