练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    11．甲、乙、丙、丁四人进行射击测试，记录每人10次射击成绩，得到各人的射击成绩平均数和方差如表中所示，则成绩最稳定的是（　　）
    统计量甲乙丙丁
    平均数9.29.29.29.2
    方差0.600.620.500.44
    A．甲B．乙C．丙D．丁

    分析 根据方差的意义可作出判断．方差是用来衡量一组数据波动大小的量，方差越小，表明这组数据分布比较集中，各数据偏离平均数越小，即波动越小，数据越稳定．

    解答 解：∵每人10次射击成绩的平均数均是9.2环，方差依次为0.60、0.62、0.50、0.44，
    ∴丁的方差最小，
    ∴成绩最稳定的是丁；
    故选D．

    点评 本题考查方差的意义．方差是用来衡量一组数据波动大小的量，方差越大，表明这组数据偏离平均数越大，即波动越大，数据越不稳定；反之，方差越小，表明这组数据分布比较集中，各数据偏离平均数越小，即波动越小，数据越稳定．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    1．下列运算正确的是（　　）
    A．（a2+2b2）-2（-a2+b2）=3a2+b2B．$\frac{{a}^{2}+1}{a-1}$-a-1=$\frac{2a}{a-1}$
    C．（-a）3m÷am=（-1）ma2mD．6x2-5x-1=（2x-1）（3x-1）

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

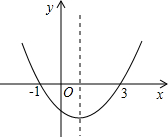    2．如图，抛物线y=ax2+bx+c（a≠0）的开口向上，与x轴交点的横坐标分别为-1、3，则下列说法错误的是（　　）
    A．对称轴是直线x=1B．方程ax2+bx+c=0的解是x1=-1，x2=3
    C．当x＜1，y随x的增大而增大D．当-1＜x＜3时，y＜0

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    19．下列计算正确的是（　　）
    A．$\sqrt{（-4）^{2}}$=2B．$\sqrt{2}$×$\sqrt{5}$=$\sqrt{10}$C．（$\sqrt{2}$）2=4D．$\sqrt{6}$÷$\sqrt{2}$=3

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    6．下列运算可直接运用平方差公式的是（　　）
    A．（a+b）（-a+b）B．（a+b）（-a-b）C．（a+b）（b+a）D．（a-b）（b-a）

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    16．已知点A（1，y1），B（2，y2），C（-3，y3）都在反比例函数y=$\frac{{{k^2}+1}}{x}$的图象上，则y1，y2，y3的大小关系是（　　）
    A．y3＜y1＜y2B．y1＜y2＜y3C．y2＜y1＜y3D．y3＜y2＜y1

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．在平面直角坐标系xOy中，抛物线y=ax2+bx+c的开口向上，且经过点A（0，$\frac{3}{2}$）
    （1）若此抛物线经过点B（2，-$\frac{1}{2}$），且与x轴相交于点E，F．
    ①填空：b=-2a-1（用含a的代数式表示）；
    ②当EF2的值最小时，求抛物线的解析式；
    （2）若a=$\frac{1}{2}$，当0≤x≤1，抛物线上的点到x轴距离的最大值为3时，求b的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．甲、乙两运动员的射击成绩（靶心为10环）统计如下表（不完全）：
    运动员
    环数
    次数    		12345
    甲1089108
    乙1099ab
    某同学计算出了甲的成绩平均数是9，方差是
    S甲2=$\frac{1}{5}$[（10-9）2+（8-9）2+（9-9）2+（10-9）2+（8-9）2]=0.8，请作答：
    （1）在图中用折线统计图将甲运动员的成绩表示出来；
    （2）若甲、乙射击成绩平均数都一样，则a+b=17；
    （3）在（2）的条件下，当甲比乙的成绩较稳定时，请列举出a、b的所有可能取值，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

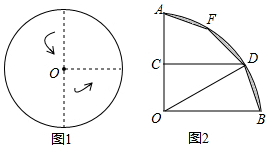    16．如图1，将一圆形纸片向右、向上两次对折后得到如图2所示的扇形AOB．已知OA=6，取OA的中点C，过点C作CD⊥OA交$\widehat{AB}$于点D，点F是$\widehat{AB}$上一点．若将扇形BOD沿OD翻折，点B恰好与点F重合，用剪刀沿着线段BD，DF，FA依次剪下，则剪下的纸片（形状同阴影图形）面积之和为36π-108．

    查看答案和解析>>

    同步练习册答案