
����Ŀ���ס���������A�س���������ʻ��B��.�׳���80km/h���ٶ���ʻ1h���ҳ�������ͬ��·��ʻ.�ҳ��ȵ���B�ز�ͣ��1h������ԭ�ٰ�ԭ·���أ�ֱ����׳�����.�ڴ˹����У�����֮��ľ���y��km�����ҳ���ʻʱ��x��h��֮��ĺ�����ϵ��ͼ��ʾ.����˵�������ҳ����ٶ���120km/h����m=160���۵�H�������ǣ�7��80������n=7.5������˵����ȷ����_________��
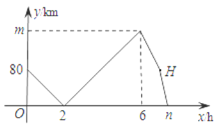
���𰸡��٢ڢ�
��������
�ٸ���ͼ��֪�ҳ���Сʱ�ϼ׳�����ʽ���㼴�ɣ�
�ڸ����ٶȲ����ʻʱ����㣻
�����A��B����֮��ľ��룬Ȼ���ȥ����ʻ�ľ������H��������ꣻ
���ɢۿ�֪H�������ǣ�7��80������ʱ�������80km��Ȼ�����������Ҫ��ʱ�䣬���ɵõ�n��ֵ.
�⣺��ס����������ٶȷֱ�ΪV����V����
�٣�V��-V������2=80����V��-V��=40km/h�����ҳ����ٶ���120km/h������ȷ��
��40����6-2��=160km����m=160������ȷ��
�۸���ͼ��֪����6Сʱ����B�أ���A��B�������120��6=720km���ҳ��ȵ���B�ز�ͣ��1h�׳�������80����1+6+1��=640km��720-640=80km�����H�������ǣ�7��80��������ȷ��
�ܵ�H�������ǣ�7��80������ʱ�������80km����80����120+80��=0.4��
��n=7+0.4=7.4���ʴ���
������˵����ȷ���ǣ��٢ڢۣ�
�ʴ�Ϊ���٢ڢ�.


 �Űٷֿ�ʱ����ϵ�д�
�Űٷֿ�ʱ����ϵ�д� ������״Ԫ��ҵϵ�д�
������״Ԫ��ҵϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ϣ�����ʦ��ʾ����ͼһ������������ͬѧ�ǵ�һ�����飬��������ĸ��۵㣺
A���������ң��˴����أ� B���������棬�˴�ƽ�⣻
C�������Ը˴˳ɾͣ� D����������������˫Ӯ��
Ҫ��ÿ��ѡȡ����һ���۵�д���Լ��ĸ�����ͬѧ�ǵ�ѡ�������С����������ͼ������������ͼ���������ͼ�����ṩ����Ϣ������������⣺
�۵� | Ƶ�� | Ƶ�� |
A | a | 0.2 |
B | 12 | 0.24 |
C | 8 | b |
D | 20 | 0.4 |

��1���μӱ������۵�ѧ�������� ���ˣ�
��2������a���� ����b���� ����
��3��������ͳ��ͼ����������
��4��������A��B��C��D�ĸ��۵�����ѡ������Ϊ�ݽ����⣬�����б�����״ͼ�ķ�����ѡ�й۵�D����������������˫Ӯ���ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A��B�Ƿ���������y��![]() ��k��0��ͼ���ϵ����㣬�ӳ��߶�AB��y���ڵ�C���ҵ�BΪ�߶�AC�е㣬����A��AD��x���ڵ�D����EΪ�߶�OD�����ȷֵ㣬��OE��DE������AE��BE����S��ABE��7����k��ֵΪ�� ��
��k��0��ͼ���ϵ����㣬�ӳ��߶�AB��y���ڵ�C���ҵ�BΪ�߶�AC�е㣬����A��AD��x���ڵ�D����EΪ�߶�OD�����ȷֵ㣬��OE��DE������AE��BE����S��ABE��7����k��ֵΪ�� ��

A.��12B.��10C.��9D.��6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y=x2-2mx+3��m��![]() ����ͼ����x�ύ�ڵ�A��a��0���͵�B��a+n��0����n��0��nΪ����������y�ύ��C�㣮
����ͼ����x�ύ�ڵ�A��a��0���͵�B��a+n��0����n��0��nΪ����������y�ύ��C�㣮
��1����a=1��������κ�����ϵʽ��������ABC�������
��2����֤��a=m-![]() ��
��
��3���߶�AB������A��B��������ֻ��������ĺ���������������a��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB��AD�ǡ�O���ң�AOƽ��![]() .����B����O�����߽�AO���ӳ����ڵ�C������CD��BO.�ӳ�BO����O�ڵ�E����AD�ڵ�F������AE��DE.
.����B����O�����߽�AO���ӳ����ڵ�C������CD��BO.�ӳ�BO����O�ڵ�E����AD�ڵ�F������AE��DE.
(1)��֤��![]() �ǡ�O�����ߣ�
�ǡ�O�����ߣ�
(2)��![]() ����
����![]() �ij�.
�ij�.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�뾶Ϊ2����O��ֱ��l�����ڵ�A����P��ֱ��AB����Բ�ϵĶ��㣬����P��ֱ��l�Ĵ��ߣ�����ΪC��PC����O���ڵ�D������PA��PB����PC�ij�Ϊx(2��x��4��
��1����![]() ʱ������PA��PB�ij��ȣ�
ʱ������PA��PB�ij��ȣ�
��2����xΪ��ֵʱ��PD��CD��ֵ������ֵ�Ƕ��٣�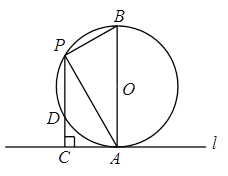
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪x1��x2��һԪ���η��̣�a��6��x2+2ax+a=0������ʵ������
��1���Ƿ����ʵ��a��ʹ��x1+x1x2=4+x2�����������ڣ����a��ֵ���������ڣ�����˵�����ɣ�
��2����ʹ��x1+1����x2+1��Ϊ��������ʵ��a������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����߳�Ϊ13������ABCD��AD����ƽ����DCEF��λ�ã���EG��AB������Ϊ��G��GD���ӳ��߽�EF�ڵ�H����֪BD��24����GH��_____��
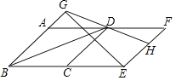
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����κ���ͼ��Ķ���Ϊ����1��1�������뷴����������ͼ���ڵ�A����3����3��
��1������κ����뷴���������Ľ���ʽ��
��2���ж�ԭ�㣨0��0���Ƿ��ڶ��κ�����ͼ���ϣ���˵�����ɣ�
��3������ͼ��ֱ��д�����κ�����ֵС�ڷ�����������ֵʱ�Ա���x��ȡֵ��Χ��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com