
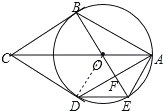
【题目】如图,AB,AD是⊙O的弦,AO平分![]() .过点B作⊙O的切线交AO的延长线于点C,连接CD,BO.延长BO交⊙O于点E,交AD于点F,连接AE,DE.
.过点B作⊙O的切线交AO的延长线于点C,连接CD,BO.延长BO交⊙O于点E,交AD于点F,连接AE,DE.
(1)求证:![]() 是⊙O的切线;
是⊙O的切线;
(2)若![]() ,求
,求![]() 的长.
的长.

【答案】(1)详见解析;(2)![]()
【解析】
(1)欲证明CD是⊙O的切线,只要证明∠CDO=∠CBO=90°,由△COB≌△COD即可解决问题.
(2)先证明∠BAO=∠OAD=∠DAE=∠ABO=30°,在Rt△AEF中利用30度性质以及勾股定理即可解决问题.
解:(1)如图,连接OD.
∵BC为圆O的切线,
∴∠CBO=90°.
∵AO平分∠BAD,
∴∠OAB=∠OAF.
∵OA=OB=OD,
∴∠OAB=∠ABO=∠OAF=∠ODA,
∵∠BOC=∠OAB+∠OBA,∠DOC=∠OAD+∠ODA,
∴∠BOC=∠DOC,
在△COB和△COD中,
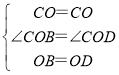 ,
,
∴BOC≌△DOC,
∴∠CBO=∠CDO=90°,
∴CD是⊙O的切线;
(2)∵AE=DE,
∴![]() ,
,
∴∠DAE=∠ABO,
∴∠BAO=∠OAD=∠ABO
∴∠BAO=∠OAD=∠DAE,
∵BE是直径,
∴∠BAE=90°,
∴∠BAO=∠OAD=∠DAE=∠ABO=30°,
∴∠AFE=90°,
在Rt△AFE中,∵AE=3,∠DAE=30°,
∴EF=![]() AE=
AE=![]() ,
,
∴AF=![]() .
.


 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案科目:初中数学 来源: 题型:
【题目】近几年购物的支付方式日益增多,某数学兴趣小组就此进行了抽样调查.调查结果显示,支付方式有:A微信、B支付宝、C现金、D其他,该小组对某超市一天内购买者的支付方式进行调查统计,得到如下两幅不完整的统计图.

请你根据统计图提供的信息,解答下列问题:
(1)本次一共调查了多少名购买者?
(2)请补全条形统计图;在扇形统计图中A种支付方式所对应的圆心角为 度.
(3)若该超市这一周内有1600名购买者,请你估计使用A和B两种支付方式的购买者共有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解七年级学生体育课足球运球的掌握情况,随机抽取部分七年级学生足球运球的测试成绩作为一个样本,按A、B、C、D四个等级进行统计,制成了如图所示的不完整的统计图:
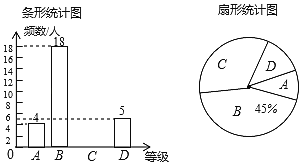
根据所给信息,解答以下问题:
(1)在扇形统计图中,求等级C对应的扇形圆心角的度数,并补全条形统计图;
(2)该校七年级有300名学生,请估计足球运球测试成绩达到A等级的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】全面两孩政策实施后,甲,乙两个家庭有了各自的规划.假定生男生女的概率相同,回答下列问题:
(1)甲家庭已有一个男孩,准备再生一个孩子,则第二个孩子是女孩的概率是 ;
(2)乙家庭没有孩子,准备生两个孩子,求至少有一个孩子是女孩的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着信息技术的快速发展,人们购物的付款方式更加多样、便捷.某校数学兴趣小组为了解人们最喜欢的付款方式设计了一份调查问卷,要求被调查者选且只选其中一种你最喜欢的付款方式.现将调查结果进行统计并绘制成如下两幅不完整的统计图,请根据统计图回答下列问题:
(1)这次活动共调查了 人;在扇形统计图中,表示“其他”付款的扇形圆心角的度数为 ;
(2)补全条形统计图;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车从A地出发,匀速驶向B地.甲车以80km/h的速度行驶1h后,乙车才沿相同线路行驶.乙车先到达B地并停留1h后,再以原速按原路返回,直至与甲车相遇.在此过程中,两车之间的距离y(km)与乙车行驶时间x(h)之间的函数关系如图所示.下列说法:①乙车的速度是120km/h;②m=160;③点H的坐标是(7,80);④n=7.5.其中说法正确的是_________.
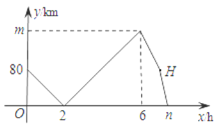
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,圆心为P(![]() ,
,![]() )的动圆经过点A(1,2)且与
)的动圆经过点A(1,2)且与![]() 轴相切于点B.
轴相切于点B.
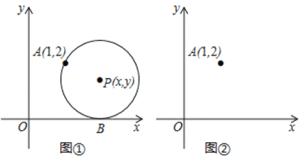
(1)当![]() =2是,求⊙P的半径;
=2是,求⊙P的半径;
(2)求![]() 关于
关于![]() 的函数解析式,在图②中画出此函数图像;
的函数解析式,在图②中画出此函数图像;
(3)请类比圆的定义(圆可以看成是到定点的距离等于定长的所有点的集合),给(2)中所得函数图像进行定义:此函数图像可以看成是到 的距离等于到 的距离的所有点的集合;
(4)当⊙P的半径为1时,若⊙P与以上(2)中所得函数图象相交于点C、D,其中交点D(![]() ,
,![]() )在点C的右侧,请利用图②,则cos∠APD= .
)在点C的右侧,请利用图②,则cos∠APD= .
查看答案和解析>>
科目:初中数学 来源: 题型:
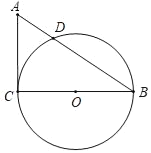
【题目】如图,在Rt△ACB中,∠C=90°,AC=3cm,BC=4cm,以BC为直径作⊙O交AB于点D,E是线段AC的中点,连接ED.
(1)求证:ED是⊙O切线.
(2)求线段AD的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列尺规作图中,能确定圆心的是( )
①如图1,在圆上任取三个点A,B,C,分别作弦AB,BC的垂直平分线,交点O即为圆心
②如图2,在圆上任取一点B,以B为圆心,小于直径长为半径画弧交圆于A,C两点连结AB,BC,作∠ABC的平分线交圆于点D,作弦BD的垂直平分线交BD于点O,点O即为圆心
③如图3,在圆上截取弦AB=CD,连结AB,BC,CD,分别作∠ABC与∠DCB的平分线,交点O即为圆心

A. ①②B. ①③C. ②④D. ①②③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com