
【题目】如图,二次函数图象的顶点为(﹣1,1),且与反比例函数的图象交于点A(﹣3,﹣3)
(1)求二次函数与反比例函数的解析式;
(2)判断原点(0,0)是否在二次函数的图象上,并说明理由;
(3)根据图象直接写出二次函数的值小于反比例函数的值时自变量x的取值范围.

【答案】(1)y=﹣(x+1)2+1,![]() ;(2)原点(0,0)是在二次函数的图象上;(3)当x<﹣3或x>0时二次函数的值小于反比例函数的值.
;(2)原点(0,0)是在二次函数的图象上;(3)当x<﹣3或x>0时二次函数的值小于反比例函数的值.
【解析】
(1)设二次函数为y=a(x+1)2+1,设反比例函数的解析式为y=![]() ,把A点的坐标代入,关键待定系数法即可求得;
,把A点的坐标代入,关键待定系数法即可求得;
(2)把x=0代入求得的二次函数的解析式即可判断;
(3)由两函数的图象直接写出x的取值范围即可.
解:(1)设二次函数为y=a(x+1)2+1,
∵经过点A(﹣3,﹣3)
∴﹣3=4a+1,
∴a=﹣1,
∴二次函数的解析式为y=﹣(x+1)2+1,
设反比例函数的解析式为y=![]() ,
,
∵二次函数的图象与反比例函数的图象交于点A(﹣3,﹣3)
∴k=﹣3×(﹣3)=9,
∴反比例函数的解析式为y=![]() ;
;
(2)把x=0代入y=﹣(x+1)2+1,得y=﹣1+1=0,
∴原点(0,0)是在二次函数的图象上;
(3)由图象可知,二次函数与反比例函数图象的交点为A(﹣3,﹣3),
当x<﹣3或x>0时二次函数的值小于反比例函数的值.


科目:初中数学 来源: 题型:
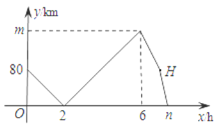
【题目】甲、乙两车从A地出发,匀速驶向B地.甲车以80km/h的速度行驶1h后,乙车才沿相同线路行驶.乙车先到达B地并停留1h后,再以原速按原路返回,直至与甲车相遇.在此过程中,两车之间的距离y(km)与乙车行驶时间x(h)之间的函数关系如图所示.下列说法:①乙车的速度是120km/h;②m=160;③点H的坐标是(7,80);④n=7.5.其中说法正确的是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校植物园沿路护栏的纹饰部分设计成若干个全等菱形图案,每增加一个菱形图案,纹饰长度就增加dcm,如图所示,已知每个菱形图案的边长为10![]() cm,其中一个内角为60°.
cm,其中一个内角为60°.
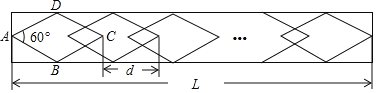
(1)求一个菱形图案水平方向的对角线长;
(2)若d=26,纹饰的长度L能否是6010cm?若能,求出菱形个数;若不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
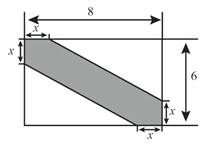
【题目】某景区内有一块矩形油菜花田地(数据如图示,单位:m.)现在其中修建一条观花道(图中阴影部分)供游人赏花.设改造后剩余油菜花地所占面积为ym2.
(1)求y与x的函数表达式;
(2)若改造后观花道的面积为13m2,求x的值;
(3)若要求 0.5≤ x ≤1,求改造后剩余油菜花地所占面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列尺规作图中,能确定圆心的是( )
①如图1,在圆上任取三个点A,B,C,分别作弦AB,BC的垂直平分线,交点O即为圆心
②如图2,在圆上任取一点B,以B为圆心,小于直径长为半径画弧交圆于A,C两点连结AB,BC,作∠ABC的平分线交圆于点D,作弦BD的垂直平分线交BD于点O,点O即为圆心
③如图3,在圆上截取弦AB=CD,连结AB,BC,CD,分别作∠ABC与∠DCB的平分线,交点O即为圆心

A. ①②B. ①③C. ②④D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形ABCD中,动点E从A出发,沿AB→BC方向运动,当点E到达点C时停止运动,过点E做FE⊥AE,交CD于F点,设点E运动路程为x,FC=y,如图2所表示的是y与x的函数关系的大致图象,当点E在BC上运动时,FC的最大长度是![]() ,则矩形ABCD的面积是( )
,则矩形ABCD的面积是( )
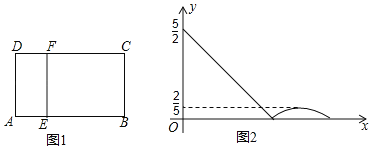
A. ![]() B. 5C. 6D.
B. 5C. 6D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于点C,顶点为D.
(1)求此抛物线的函数表达式;
(2)以点B为直角顶点作直角三角形BCE,斜边CE与抛物线交于点P,且CP=EP,求点P的坐标;
(3)△BOC绕着它的顶点B顺时针在第一象限内旋转,旋转的角度为α,旋转后的图形为△BO1C1.当旋转后的△BO1C1有一边在直线BD上时,求△BO1C1不在BD上的顶点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学兴趣小组的活动中,小明进行数学探究活动,将边长为2的正方形ABCD与边长为2![]() 的正方形AEFG按图①位置放置,AD与AE在同一直线上,AB与AG在同一直线上.
的正方形AEFG按图①位置放置,AD与AE在同一直线上,AB与AG在同一直线上.
⑴小明发现DG⊥BE,请你帮他说明理由.
⑵如图②,小明将正方形ABCD绕点A逆时针旋转,当点B恰好落在线段DG上时,请你帮他求出此时BE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在ABCD中,DE平分∠ADB,交AB于E,BF平分∠CBD,交CD于F.
(1)求证:△ADE≌△CBF;
(2)当AD与BD满足什么关系时,四边形DEBF是矩形?请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com