
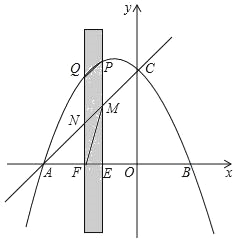
����Ŀ����ͼ��������y�T��![]() x2+bx+c��x�ύ�ڵ�A�͵�B����y�ύ�ڵ�C����B������Ϊ��3��0������C������Ϊ��0��5������һ����Ϊ1�������㹻���ľ��Σ���Ӱ���֣���x�᷽��ƽ�ƣ���y��ƽ�е�һ��Ա߽��������ڵ�P�͵�Q����ֱ��AC�ڵ�M�͵�N����x���ڵ�E�͵�F��
x2+bx+c��x�ύ�ڵ�A�͵�B����y�ύ�ڵ�C����B������Ϊ��3��0������C������Ϊ��0��5������һ����Ϊ1�������㹻���ľ��Σ���Ӱ���֣���x�᷽��ƽ�ƣ���y��ƽ�е�һ��Ա߽��������ڵ�P�͵�Q����ֱ��AC�ڵ�M�͵�N����x���ڵ�E�͵�F��
��1���������ߵĽ���ʽ����A�����ꣻ
��2������M��N�����߶�AC��ʱ������MF�����sin��AMF=![]() �����Q�����ꣻ
�����Q�����ꣻ
��3���ھ��ε�ƽ�ƹ����У��Ƿ�����Ե�P��Q��M��NΪ������ı�����ƽ���ı��Σ������ڣ������M�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��y=��![]() x2��
x2��![]() x+5����A�������ǣ���5��0������2����Q���꣨��4��
x+5����A�������ǣ���5��0������2����Q���꣨��4��![]() ������3���Ե�P��Q��M��NΪ������ı�����ƽ���ı���ʱ����M������Ϊ����2��3����2+
������3���Ե�P��Q��M��NΪ������ı�����ƽ���ı���ʱ����M������Ϊ����2��3����2+![]() ��3+
��3+![]() ����2��
����2��![]() ��3��
��3��![]() ����
����
��������
(1)�ѵ�B��C��������뺯������ʽ���b��c��ֵ�����������A�����꼴��;(2) ��FG��AC��G , ���F���꣨m��0��������sin��AMF=![]() ���г����̽��; (3)������������ۢٵ�MN�ǶԽ���ʱ���ڵ�MNΪ��ʱ�����.
���г����̽��; (3)������������ۢٵ�MN�ǶԽ���ʱ���ڵ�MNΪ��ʱ�����.
��1�����������ϵĵ�B������Ϊ��3��0������C������Ϊ��0��5��
�ཫ�����y�T��![]() x2+bx+c����
x2+bx+c����
![]() ��
��
���b=��![]() ��c=5��
��c=5��
�������ߵĽ���ʽΪy=��![]() x2��
x2��![]() x+5��
x+5��
���A�������ǣ���5��0����
��2����FG��AC��G��
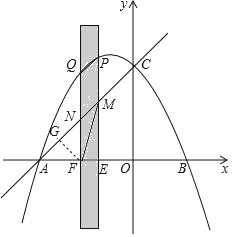
���F���꣨m��0����
��AF=m+5��AE=EM=m+6��FG=![]() ��m+5����FM=
��m+5����FM=![]() ��
��
��sin��AMF=![]() ��
��
��=![]() ��
��
��![]() =
=![]() ��
��
�����õ�2m2+19m+44=0��
�ࣨm+4����2m+11��=0��
��m=��4��5.5����������
���Q���꣨��4��![]() ����
����
��3���ٵ�MN�ǶԽ���ʱ����M��y����Ҳ࣬���F��m��0����
��ֱ��AC����ʽΪy=x+5��
���N��m��m+5������M��m+1��m+6����
��QN=PM��
�ੁ![]() m2��
m2��![]() m+5��m��5=m+6��[��
m+5��m��5=m+6��[��![]() ��m+1��2��
��m+1��2��![]() ��m+1��+5]��
��m+1��+5]��
���m=��3+![]() ����3��
����3��![]() ����������
����������
��ʱM����2+![]() ��3+
��3+![]() ����
����
��MN�ǶԽ���ʱ����N�ڵ�A�����ʱ�����F��m��0����
��m+5������![]() m2��
m2��![]() m+5��=[��
m+5��=[��![]() ��m+1��2��
��m+1��2��![]() ��m+1��+5]����m+6����
��m+1��+5]����m+6����
���m=��3��![]() ��3+
��3+![]() ����������
����������
��ʱM����2��![]() ��3��
��3��![]() ��
��
�ڵ�MNΪ��ʱ�����Q��m����![]() m2��
m2��![]() m+5�����P��m+1����
m+5�����P��m+1����![]() m2��
m2��![]() m+6����
m+6����
��NQ=PM��
�ੁ![]() m2��
m2��![]() m+6=��
m+6=��![]() ��m+1��2��
��m+1��2��![]() ��m+1��+5��
��m+1��+5��
���m=��3��
���M���꣨��2��3����
���������Ե�P��Q��M��NΪ������ı�����ƽ���ı���ʱ����M������Ϊ����2��3����2+![]() ��3+
��3+![]() ����2��
����2��![]() ��3��
��3��![]() ����
����


 Сѧ��10���ӿ������100��ϵ�д�
Сѧ��10���ӿ������100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ABC�У�AC=BC����ACB=90����D��E��ֱ��AB�����㣮��DCE=45��
��1����CE��ABʱ����D���A�غϣ���֤��DE2=AD2+BE2
��2����AB=4ʱ�����E���߶�AC����̾���
��3������D�����A�غ�ʱ��̽����DE2=AD2+BE2�Ƿ����������������֤����������������˵������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
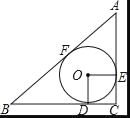
����Ŀ����ͼ����ABC�У���C=90�㣬��O�ǡ�ABC������Բ��D��E��F���е㣮
��1����֤���ı���ODCE�������Σ�
��2�����AC=6��BC=8��������Բ��O�İ뾶��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���п����ڲ���ǰ��ij��������Ϊ���˽�ѡ���������ϵľ��꼶�����ijɼ�������������˱�������ѡ������������Ŀ�ľ��꼶�����ijɼ����������Եõ��ijɼ����������������������ͳ��ͼ��
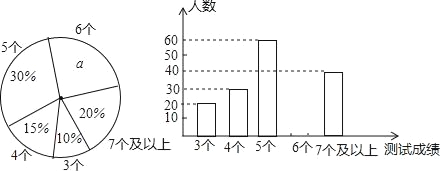
�������ͼ�е���Ϣ������������⣺
����д������ͼ��a=����%�����γ���У��ɼ�Ϊ6����ѧ������������
��������γ���У����Գɼ���ƽ��������������λ����
�����������п�ѡ���������ϵ���������1800�ˣ���������п��������ϴ�6�����ϣ���6���������֣�������Ƹ��������п�ѡ���������ϵ������ܻ�����ֵ��ж�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���״�վC����һö�ɵ��洹ֱ���յ�Ѳ��������������240m/s���ٶȣ���10��ӵ�A���е���B����C����õ�A��B�����Ƿֱ�Ϊ34����45����������λ��O���״�վC֮��ľ��루�����ȷ��0.1km�������ο����ݣ�sin34���0.56��cos34���0.83��tan34���0.67��
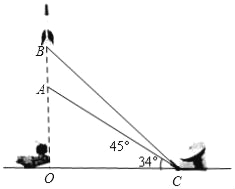
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
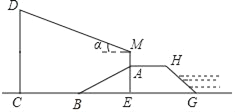
����Ŀ����ͼ�������̵ĺ����ABGH�����Σ���ˮ��AB���¶�i=1��![]() ����ֱ�߶�AE��ˮƽ����BE�ıȣ���AB=20�ף�BC=30�ף�����Ϊ1.7��С����AM=1.7�ף�վ�ڴ��A�㣨M��A��E������ͬһ��ֱ���ϣ�����õ��߸˶���D�����ǡ�a=20�㣮
����ֱ�߶�AE��ˮƽ����BE�ıȣ���AB=20�ף�BC=30�ף�����Ϊ1.7��С����AM=1.7�ף�վ�ڴ��A�㣨M��A��E������ͬһ��ֱ���ϣ�����õ��߸˶���D�����ǡ�a=20�㣮
��1����ˮ��AB���½ǣ�
��2������߸�CD�ĸ߶ȣ��������ȷ����λ���ο�����sin20����0.3��cos20����0.9��tan20����0.4��![]() ��1.7��
��1.7��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,��֪��ABC,��C=90��,�����²��裺�ٷֱ���A.BΪԲ��,�Դ���![]() AB�ij�Ϊ�뾶����,�����ཻ������M��N;����ֱ��MN��BC�ڵ�D. ��AC=1.5,��B=15��.��BD����( )
AB�ij�Ϊ�뾶����,�����ཻ������M��N;����ֱ��MN��BC�ڵ�D. ��AC=1.5,��B=15��.��BD����( )

A.1.5B.2C.2.5D.3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪,��ͼ��ABC��,��ABC=45��,AB=BC��CD��AB��D��BEƽ�֡�ABC����BE��AC��E����CD�ཻ�ڵ�F.H��BC�ߵ��е㣬����DH��BE�ཻ�ڵ�G��

(1)��֤BF=AC��
(2)��֤CE=![]() BF.
BF.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() Ϊ�ȱ������Σ�
Ϊ�ȱ������Σ�![]() Ϊ
Ϊ![]() �ĸߣ��ӳ�
�ĸߣ��ӳ�![]() ��
��![]() ��ʹ
��ʹ![]() ������
������![]() ����
����![]() __________��
__________��![]() __________��
__________��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com