
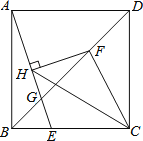
【题目】在正方形ABCD中,点E为BC边上一点且CE=2BE,点F为对角线BD上一点且BF=2DF,连接AE交BD于点G,过点F作FH⊥AE于点H,连结CH、CF,若HG=2cm,则△CHF的面积是______cm2.
【答案】![]()
【解析】
如图,过F作FI⊥BC于I,连接FE,FA,得到FI∥CD,设BE=EI=IC=a,CE=FI=2a,AB=3a,由勾股定理得到FE=FC=FA=![]() a,推出HE=
a,推出HE=![]() AE=
AE=![]() a,根据正方形的性得到BG平分∠ABC,由三角形角平分线定理得到
a,根据正方形的性得到BG平分∠ABC,由三角形角平分线定理得到![]() ,求得HG=
,求得HG=![]() AE=
AE=![]() a=2,于是得到结论.
a=2,于是得到结论.
解:如图,过F作FI⊥BC于I,连接FE,FA,
∴FI∥CD,
∵CE=2BE,BF=2DF,
∴设BE=EI=IC=a,CE=FI=2a,AB=3a,
∴则FE=FC=FA=![]() a,
a,
∴H为AE的中点,
∴HE=![]() AE=
AE=![]() a,
a,
∵四边形ABCD是正方形,
∴BG平分∠ABC,
∴![]()
∴HG=![]() AE=
AE=![]() a=2,
a=2,
∴a=![]() ,
,
∴S△CHF=S△HEF+S△CEF-S△CEH=![]() (
(![]() a)2+
a)2+![]() 2a2a-
2a2a-![]() 2a
2a![]() a=
a=![]() a2=
a2=![]() ,
,

故答案为:![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】现有四张质地均匀,大小完全相同的卡片,在其正面分别标有数字﹣1,﹣2,2,3,把卡片背面朝上洗匀,从中随机抽出一张后,不放回,再从中随机抽出一张,则两次抽出的卡片所标数字之和为正数的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校想了解学生每周的课外阅读时间情况,随机调查了部分学生,对学生每周的课外阅读时间x(单位:小时)进行分组整理,并绘制了如图所示的不完整的频数分别直方图和扇形统计图:

根据图中提供的信息,解答下列问题:
(1)补全频数分布直方图
(2)求扇形统计图中m的值和E组对应的圆心角度数
(3)请估计该校3000名学生中每周的课外阅读时间不小于6小时的人数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行2400米,先到终点的人原地休息.已知甲先出发4分钟,在整个步行过程中,甲、乙两人的距离y(米)与甲出发的时间t(分)之间的关系如图所示,下列结论:
①甲步行的速度为60米/分;
②乙走完全程用了32分钟;
③乙用16分钟追上甲;
④乙到达终点时,甲离终点还有300米
其中正确的结论有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题背景:在![]() 中,
中,![]() 边上的动点
边上的动点![]() 由
由![]() 向
向![]() 运动(与
运动(与![]() ,
,![]() 不重合),点
不重合),点![]() 与点
与点![]() 同时出发,由点
同时出发,由点![]() 沿
沿![]() 的延长线方向运动(
的延长线方向运动(![]() 不与
不与![]() 重合),连结
重合),连结![]() 交
交![]() 于点
于点![]() ,点
,点![]() 是线段
是线段![]() 上一点.
上一点.
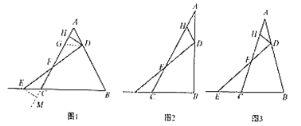
(1)初步尝试:如图,若![]() 是等边三角形,
是等边三角形,![]() ,且点
,且点![]() ,
,![]() 的运动速度相等,求证:
的运动速度相等,求证:![]() .
.
小王同学发现可以由以下两种思路解决此问题:
思路一:过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,先证
,先证![]() ,再证
,再证![]() ,从而证得结论成立;
,从而证得结论成立;
思路二:过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,先证
,先证![]() ,再证
,再证![]() ,从而证得结论成立.
,从而证得结论成立.
请你任选一种思路,完整地书写本小题的证明过程(如用两种方法作答,则以第一种方法评分)
(2)类比探究:如图,若在![]() 中,
中,![]() ,
,![]() ,且点
,且点![]() ,
,![]() 的运动速度之比是
的运动速度之比是![]() ,求
,求![]() 的值;
的值;
(3)延伸拓展:如图,若在![]() 中,
中,![]() ,
,![]() ,记
,记![]() ,且点
,且点![]() 、
、![]() 的运动速度相等,试用含
的运动速度相等,试用含![]() 的代数式表示
的代数式表示![]() (直接写出结果,不必写解答过程).
(直接写出结果,不必写解答过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
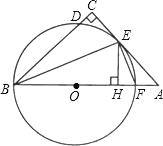
【题目】如图,在△ABC中,∠C=90°,∠ABC的平分线交AC于点E,过点E作BE的垂线交AB于点F,⊙O是△BEF的外接圆.
(1)求证:AC是⊙O的切线;
(2)过点E作EH⊥AB,垂足为H,求证:CD=HF;
(3)若CD=1,EH=3,求BF及AF长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个红色不透明的盒子中放有四张分别写有数字1,2,3,4的红色卡片,在一个蓝色不透明的盒子中放有三张分别写有数字1,2,3的蓝色卡片,卡片除颜色和数字外完全相同.
(1)从红盒中任意抽取一张红色卡片,从蓝盒中任意抽取一张蓝色卡片,用列举法(树形图或列表法)表示所有的可能情况;
(2)求两张卡片上写有相同数字的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一张正方形纸的内部被针扎了2010个孔,这些孔和正方形的顶点之中的任何3点都不共线.作若干条互不相交的线段,它们的端点都是这些孔或正方形的顶点,这些线段将正方形分割成一些三角形,并且在这些三角形的内部和边上都不再有小孔.请问一共作了多少条线段?共得到了多少个三角形?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com