

���� �Ķ����⣺��ͼ1�У���A��AF��AD����AF=AD������CF��EF���ɡ�EAD�ա�EAF���Ƴ�DE=EF���ɡ�BAD+��CAE=45�㣬��CAE+��CAF=45�㣬�Ƴ���BAD=��CAE���ɡ�BAD�ա�CAF���Ƴ�BD=CF����B=��ACF=45�㣬��EF2=EC2+CF2�������Ƴ�DE2=BD2+CE2��
��չӦ�ã���ͼ2�У����ۣ����߶�BE��CD��DE�ij���Ϊ���߳�����������ֱ�������Σ���AF��AE��ʹ��AF=AE������DF��CF��ֻҪ֤����FAC�ա�EAB����DAF�ա�DAE�����ɽ�����⣮
��� �Ķ����⣺֤������ͼ1�У���A��AF��AD����AF=AD������CF��EF��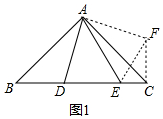
�ߡ�DAE=45�㣬��DAF=90�㣬
���DAE=��EAF=45�㣬
�ڡ�EAD�͡�EAF�У�
$\left\{\begin{array}{l}{EA=EA}\\{��EAD=��EAF}\\{AD=AF}\end{array}\right.$��
���EAD�ա�EAF��
��DE=EF��
�ߡ�BAD+��CAE=45�㣬��CAE+��CAF=45�㣬
���BAD=��CAE��
�ڡ�BAD�͡�CAE�У�
$\left\{\begin{array}{l}{AB=AC}\\{��BAD=��CAF}\\{AD=AF}\end{array}\right.$��
���BAD�ա�CAF��
��BD=CF����B=��ACF=45�㣬
�ߡ�ACB=45�㣬
���ECF=90�㣬
��EF2=EC2+CF2��
��DE2=BD2+CE2��
��չӦ�ã��⣺��ͼ2�У����ۣ����߶�BE��CD��DE�ij���Ϊ���߳�����������ֱ�������Σ�
���ɣ���AF��AE��ʹ��AF=AE������DF��CF��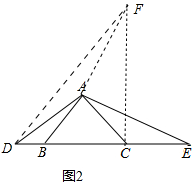
�ߡ�EAF=��BAC=90�㣬
���FAC=��EAB��
�ڡ�FAC�͡�EAB�У�
$\left\{\begin{array}{l}{AF=AE}\\{��FAC=��EAB}\\{AC=AB}\end{array}\right.$��
���FAC�ա�EAB��
��BE=CF����ACF=��EBA=45�㣬
�ߡ�ACB=45�㣬
���FCB=90�㣬
�ߡ�DAE=135�㣬��EAF=90�㣬
���DAF=360��-135��-90��=135�㣬
���DAF=��DAE��
��AD=AD��AF=AE��
���DAF�ա�DAE��
��DF=DE��
��Rt��DCF����DF2=DC2+CF2��
��DE2=DC2+BE2��
�����߶�BE��CD��DE�ij���Ϊ���߳�����������ֱ�������Σ�
���� ���⿼�������������ε��ж������ʣ�ȫ�������ε��ж������ʣ�����ֱ�������ε����ʣ����ɶ�����֪ʶ������Ĺؼ���ѧ�����ӳ��ø����ߣ�����ȫ�������ν�����⣬ѧ����ת����˼��˼�����⣬�����п�ѹ���⣮


 �ο�������ϵ�д�
�ο�������ϵ�д� ������ѧ��ʱ��ҵϵ�д�
������ѧ��ʱ��ҵϵ�д� ���������ʱ��ѵϵ�д�
���������ʱ��ѵϵ�д� �㽭�¿γ���άĿ�������ʱ��ѵϵ�д�
�㽭�¿γ���άĿ�������ʱ��ѵϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x3•��-x��3=��-x��6 | B�� | x10��x2=x5 | C�� | ��a+b��2=a2+b2 | D�� | ��2x3��2=4x6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��15x2y-5xy2����5xy=3x-5y | B�� | 98��102=��100-2����100+2��=9996 | ||
| C�� | $\frac{x}{x+3}-1=\frac{3}{x+3}$ | D�� | ��3x+1����x-2��=3x2+x-2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ����ƽ��ֱ������ϵ�У�A��1��0����B��0��2������ABΪ���ڵ�һ������������ABCD����Dǡ������˫����y=$\frac{k}{x}$�ϣ���k��ֵ�ǣ�������
��ͼ����ƽ��ֱ������ϵ�У�A��1��0����B��0��2������ABΪ���ڵ�һ������������ABCD����Dǡ������˫����y=$\frac{k}{x}$�ϣ���k��ֵ�ǣ�������| A�� | 4 | B�� | 3 | C�� | 2 | D�� | 1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | y=-2��x+1��2 | B�� | y=-2��x-1��2 | C�� | y=-2x2+1 | D�� | y=-2x2-1 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com