
【题目】如图,线段AB=8cm,射线AN⊥AB,垂足为点A,点C是射线上一动点,分别以AC,BC为直角边作等腰直角三角形,得△ACD与△BCE,连接DE交射线AN于点M,则CM的长为__________.
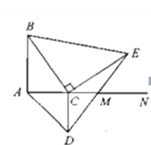
【答案】4cm.
【解析】
过点E作EF⊥AN于F,先利用AAS证出△ABC≌△FCE,从而得出AB=FC=8cm,AC=FE,然后利用AAS证出△DCM≌△EFM,从而求出CM的长.
解:过点E作EF⊥AN于F,如图所示
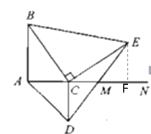
∵AN⊥AB,△BCE和△ACD为等腰直角三角形,
∴∠BAC=∠BCE=∠ACD=∠CFE =90°,BC=CE,AC=CD
∴∠ABC+∠ACB=90°,∠FCE+∠ACB =90°,
∴∠ABC =∠FCE,
在△ABC和△FCE中
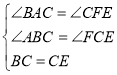
∴△ABC≌△FCE
∴AB=FC=8cm,AC=FE
∴CD= FE
在△DCM和△EFM中
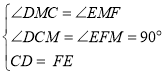
∴△DCM≌△EFM
∴CM=FM=![]() FC=4cm.
FC=4cm.
故答案为:4cm.


 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:初中数学 来源: 题型:
【题目】已知二次函数![]() (a≠0)的图象如图所示,
(a≠0)的图象如图所示,
有下列结论:
①a、b同号;
②当x=1和x=3时,函数值相等;
③4a+b=0;
④当-1<x<5时,y<0.
其中正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一棵树CD的10m高处的B点有两只猴子,它们都要到A处池塘边喝水,其中一只猴子沿树爬下走到离树20m处的池塘A处,另一只猴子爬到树顶D后直线跃入池塘的A处.如果两只猴子所经过的路程相等,试问这棵树多高?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是售货员与小丽的对话:

根据对话内容解答下列问题:
(1)A,B两种文具的单价各是多少元?
(2)若购买A,B两种文具共20件,其中A种文具的数量少于10件,且购买总费用不超过260元,共有哪几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D是BC的中点,作射线AD,在线段AD及其延长线上分别取点E,F,连结CE,BF.添加一个条件,使得△BDF≌△CDE,你添加的条件是_____________________(不添加辅助线).
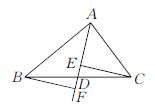
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在锐角三角形ABC中,直线l为BC的中垂线,射线m为∠ABC的角平分线,直线l与m相交于点P.若∠BAC=60°,∠ACP=24°,则∠ABP的度数是( )

A. 24° B. 30° C. 32° D. 36°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,∠BAC=90°,AB=AC,F是BC上一点,BD
中,∠BAC=90°,AB=AC,F是BC上一点,BD![]() AF的延长线与D,CE
AF的延长线与D,CE![]() AF于E,已知CE=5,BD=2,ED=__________
AF于E,已知CE=5,BD=2,ED=__________
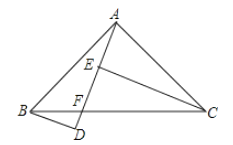
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,过等边三角形ABC边AB上一点D作DE∥BC交边AC于点E,分别取BC,DE的中点M,N,连接MN.
(1)发现:在图1中,![]() ,说明理由;
,说明理由;
(2)探索:如图2,将△ADE绕点A旋转,请求出![]() 的值;
的值;
(3)拓展:如图3,△ABC和△ADE是等腰三角形,且∠BAC=∠DAE,M,N分别是底边BC,DF的中点,若BD⊥CE,请直接写出![]() 的值.
的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com