
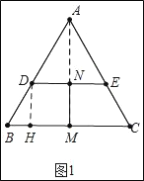
【题目】如图1,过等边三角形ABC边AB上一点D作DE∥BC交边AC于点E,分别取BC,DE的中点M,N,连接MN.
(1)发现:在图1中,![]() ,说明理由;
,说明理由;
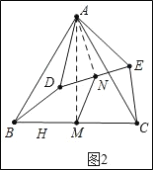
(2)探索:如图2,将△ADE绕点A旋转,请求出![]() 的值;
的值;
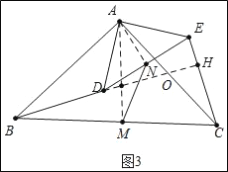
(3)拓展:如图3,△ABC和△ADE是等腰三角形,且∠BAC=∠DAE,M,N分别是底边BC,DF的中点,若BD⊥CE,请直接写出![]() 的值.
的值.

【答案】(1)详见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)如图1中,作DH⊥BC于H,连接AM,只要证明四边形MNDH是矩形,即可解出答案;
(2)如图2中,连接AM、AN,只要证明△BAD∽△MAN,利用相似比![]() 即可解出答案;
即可解出答案;
(3)如图3中,连接AM、AN,延长AD交CE于H,交AC于O,由△BAD∽△MAN,推出![]() =
=![]() =sin∠ABC,只要证明△ABC是等腰直角三角形即可解出答案.
=sin∠ABC,只要证明△ABC是等腰直角三角形即可解出答案.
(1)如图1中,作DH⊥BC于H,连接AM.
∵AB=AC,BM=CM,
∴AM⊥BC,
∵△ADE时等边三角形,
∴∠ADE=60°=∠B,
∴DE∥BC,
∵AM⊥BC,
∴AM⊥DE,
∴AM平分线段DE,
∵DN=NE,
∴A、N、M共线,
∴∠NMH=∠MND=∠DHM=90°,
∴四边形MNDH是矩形,
∴MN=DH,
∴![]() =
=![]() =sin60°=
=sin60°=![]() ;
;
(2)如图2中,连接AM、AN.
∵△ABC,△ADE都是等边三角形,BM=MC,DN=NE,
∴AM⊥BC,AN⊥DE,
∴![]() =sin60°,
=sin60°,![]() =sin60°,
=sin60°,
∴![]() =
=![]() ,
,
∵∠MAB=∠DAN=30°,
∴∠BAD=∠MAN,
∴△BAD∽△MAN,
∴![]() =
=![]() =sin60°=
=sin60°=![]() .
.
(3)如图3中,连接AM、AN,延长AD交CE于H,交AC于O.
∵AB=AC,AD=AE,BM=CM,DN=NE,
∴AM⊥BC,AN⊥DE,
∵∠BAC=∠DAE,
∴∠ABC=∠ADE,
∴sin∠ABM=sin∠ADN,
∴![]() =
=![]() ,
,
∵∠BAM=![]() BAC,∠DAN=
BAC,∠DAN=![]() ∠DAE,
∠DAE,
∴∠BAM=∠DAN,
∴∠BAD=∠MAN.
∴△BAD∽△MAN,
∴![]() =
=![]() =sin∠ABC,
=sin∠ABC,
∵∠BAC=∠DAE,
∴∠BAD=∠CAE,
∵AB=AC,AD=AE,
∴△BAD≌△CAE,
∴∠ABD=∠ACE,
∵BD⊥CE,
∴∠BHC=90°,
∴∠ACE+∠COH=90°,∵∠AOB=∠COH,
∴∠ABD+∠AOB=90°,
∴∠BAO=90°,
∵AB=AC,
∴∠ABC=45°,
∴![]() =sin45°=
=sin45°=![]() .
.


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:
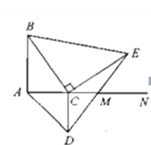
【题目】如图,线段AB=8cm,射线AN⊥AB,垂足为点A,点C是射线上一动点,分别以AC,BC为直角边作等腰直角三角形,得△ACD与△BCE,连接DE交射线AN于点M,则CM的长为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
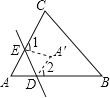
【题目】如图,小李制作了一张△ABC纸片,点D、E分别在边AB、AC上,现将△ABC沿着DE折叠压平,使点A落在点A′位置.若∠A=75°,则∠1+∠2= .
查看答案和解析>>
科目:初中数学 来源: 题型:
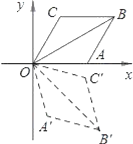
【题目】如图,菱形OABC的一边OA在x轴上,将菱形OABC绕原点O顺时针旋转75°至OA’B’C’的位置.若OB=![]() ,∠C=120°,则点B’的坐标为( )
,∠C=120°,则点B’的坐标为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在线段
在线段![]() 上运动(
上运动(![]() 不与
不与![]() ,
,![]() 重合),连接
重合),连接![]() ,
,![]() ,
,![]() 交线段
交线段![]() 于
于![]() .
.
(1)当![]() 时,
时,![]() ______
______![]() ,
,![]() ______
______![]() ,点
,点![]() 从
从![]() 向
向![]() 运动时,
运动时,![]() 逐渐变______(填“大”或“小”);
逐渐变______(填“大”或“小”);
(2)当![]() 等于多少时,
等于多少时,![]() 与
与![]() 全等?请说明理由.
全等?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,以原点O为圆心的圆过点A(5,0),直线y=kx-2k+3(k≠0)与⊙O交于B、C两点,则弦BC的长的最小值为____.

查看答案和解析>>
科目:初中数学 来源: 题型:
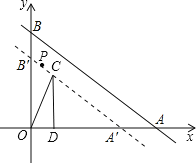
【题目】如图,已知点A、B分别在x轴、y轴上,AB=12,∠OAB=30°,经过A、B的直线l以每秒1个单位的速度向下作匀速平移运动,与此同时,点P从点B出发,在直线l上以每秒1个单位的速度沿直线l向右下方向作匀速运动.设它们运动的时间为t秒.
(1)直接写出A、B点坐标是A点 ,B点 ;
(2)用含t的代数式求出表示点P的坐标;
(3)过O作OC⊥l于C,过C作CD⊥x轴于D,问:t为何值时,以P为圆心、1为半径的圆与直线OC相切?并写出此时⊙P与直线CD的位置关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
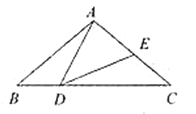
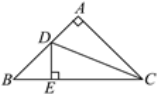
【题目】如图,在△ABC中,∠A=90°,AC=AB,CD平分∠ACB,DE⊥BC于点E,若BC=15 cm,则△DEB的周长为( )
A.14 cmB.15 cm
C.16 cmD.17 cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小王剪了两张直角三角形纸片,进行了如下的操作:

操作一:如图1,将Rt△ABC沿某条直线折叠,使斜边的两个端点A与B重合,折痕为DE.
(1)如果AC=6cm,BC=8cm,可求得△ACD的周长为 ;
(2)如果∠CAD:∠BAD=4:7,可求得∠B的度数为 ;
操作二:如图2,小王拿出另一张Rt△ABC纸片,将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,若AC=9cm,BC=12cm,请求出CD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com