
【题目】科幻小说《实验室的故事》中,有这样一个情节:科学家把一种珍奇的植物分别放在不同温度的环境中,经过一天后,测试出这种植物高度的增长情况(如下表).

由这些数据,科学家推测出植物每天高度增长量y是温度x的函数.且这种函数是反比例函数、一次函数和二次函数中的一种.
(1)请你选择一种适当的函数,求出它的函数关系式,并简要说明不选择另外两种函数的理由;
(2)温度为多少时,这种植物每天高度的增长量最大?
(3)如果实验室温度保持不变,在10天内要使该植物高度增长量的总和超过250mm,那么实验室的温度x应该在哪个范围内选择?请直接写出结果.
【答案】(1)选择二次函数,![]() ,理由见解析;(2)-1℃;(3)-6℃<x<4℃.
,理由见解析;(2)-1℃;(3)-6℃<x<4℃.
【解析】
(1)选择二次函数,设![]() (
(![]() ),然后选择
),然后选择![]() 、
、![]() 、
、![]() 三组数据,利用待定系数法求二次函数解析式即可,再根据反比例函数的自变量
三组数据,利用待定系数法求二次函数解析式即可,再根据反比例函数的自变量![]() 不能为
不能为![]() ,一次函数的特点,即可排除另两种函数;
,一次函数的特点,即可排除另两种函数;
(2)把二次函数解析式整理成顶点式形式,再根据二次函数的最值问题解答;
(3)求出平均每天的高度增长量为![]() ,然后根据
,然后根据![]() 求出
求出![]() 的值,再根据二次函数的性质写出
的值,再根据二次函数的性质写出![]() 的取值范围.
的取值范围.
(1)选择二次函数,设![]() (
(![]() ),
),
∵![]() 时,
时,![]() ;
;
![]() 时,
时,![]() ;
;
![]() 时,
时,![]() ,
,
∴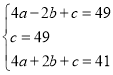 ,
,
解得: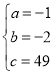 ,
,
∴y关于x的函数关系式为![]() ;
;
不选另外两个函数的理由:
∵点(0,49)不可能在反比例函数图象上,
∴y不是x的反比例函数;
∵点(-4,41),(-2,49),(2,41)不在同一直线上,
∴y不是x的一次函数;
(2)由(1)得:![]() .
.
∵![]() ,
,
∴当![]() 时,y有最大值为50,
时,y有最大值为50,
即当温度为-1℃时,这种作物每天高度增长量最大;
(3)![]()
![]() 天内要使该植物高度增长量的总和超过
天内要使该植物高度增长量的总和超过![]() ,
,
![]() 平均每天该植物高度增长量超过
平均每天该植物高度增长量超过![]() ,
,
当![]() 时,
时,![]() ,
,
整理得,![]() ,
,
解得![]() ,
,![]() ,
,
![]() 在10天内要使该植物高度增长量的总和超过
在10天内要使该植物高度增长量的总和超过![]() ,实验室的温度应保持在
,实验室的温度应保持在![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,有一个由六个边长为1的正方形组成的图案,其中点A,B的坐标分别为(3,5),(6,1).若过原点的直线l将这个图案分成面积相等的两部分,则直线l的函数解析式为_____.
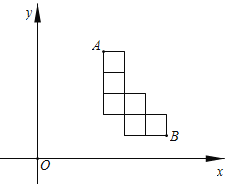
查看答案和解析>>
科目:初中数学 来源: 题型:
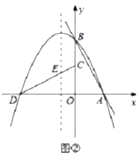
【题目】如图①,定义:直线![]() 与x、y轴分别相交于A、B两点,将
与x、y轴分别相交于A、B两点,将![]() 绕着点O逆时针旋转90°得到
绕着点O逆时针旋转90°得到![]() ,过点A、B、D的抛物线P叫做直线
,过点A、B、D的抛物线P叫做直线![]() 的“纠缠抛物线”,反之,直线
的“纠缠抛物线”,反之,直线![]() 叫做P的“纠缠直线",两线“互为纠缠线”.
叫做P的“纠缠直线",两线“互为纠缠线”.
(1)若![]() ,则纠缠物线P的函数解析式是____________.
,则纠缠物线P的函数解析式是____________.
(2)判断并说明![]() 与
与![]() 是否“互为纠缠线”.
是否“互为纠缠线”.
(3)如图②,若纠缠直线![]() ,纠缠抛物线P的对称轴与
,纠缠抛物线P的对称轴与![]() 相交于点E,点F在
相交于点E,点F在![]() 上,点Q在P的对称轴上,当以点C、E、Q、F为顶点的四边形是以
上,点Q在P的对称轴上,当以点C、E、Q、F为顶点的四边形是以![]() 为一边的平行四边形时,求点Q的坐标.
为一边的平行四边形时,求点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用A、B两种机器人搬运大米,A型机器人比B型机器人每小时多搬运20袋大米,A型机器人搬运700袋大米与B型机器人搬运500袋大米所用时间相等.求A、B型机器人每小时分别搬运多少袋大米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,对于点P(x,y)和Q(x,y′),给出如下定义:如果y′=![]() ,那么称点Q为点P的“伴随点”.
,那么称点Q为点P的“伴随点”.
例如:点(5,6)的“伴随点”为点(5,6);点(﹣5,6)的“伴随点”为点(﹣5,﹣6).
(1)直接写出点A(2,1)的“伴随点”A′的坐标.
(2)点B(m,m+1)在函数y=kx+3的图象上,若其“伴随点”B′的纵坐标为2,求函数y=kx+3的解析式.
(3)点C、D在函数y=﹣x2+4的图象上,且点C、D关于y轴对称,点D的“伴随点”为D′.若点C在第一象限,且CD=DD′,求此时“伴随点”D′的横坐标.
(4)点E在函数y=﹣x2+n(﹣1≤x≤2)的图象上,若其“伴随点”E′的纵坐标y′的最大值为m(1≤m≤3),直接写出实数n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】去年冬天,我市遭遇大雪,为确保道路正常通行,市政府启用了铲雪车清理道路,已知一台铲雪车的工作效率相当于一名环卫工人的![]() 倍,一台铲雪车清理
倍,一台铲雪车清理![]() 立方米的积雪,要比
立方米的积雪,要比![]() 名环卫工人清理这些积雪少用
名环卫工人清理这些积雪少用![]() 小时.
小时.
(1)求一台铲雪车每小时清雪多少立方米?
(2)现有一项清理任务,要求不超过![]() 小时完成
小时完成![]() 立方米的积需清理,市政府调配了
立方米的积需清理,市政府调配了![]() 台铲雪车和
台铲雪车和![]() 名环卫工人,工作了
名环卫工人,工作了![]() 小时后,又调配了一些铲雪车进行支援,则市政府至少又调配了几台铲雪车才能完成任务?
小时后,又调配了一些铲雪车进行支援,则市政府至少又调配了几台铲雪车才能完成任务?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是

A.AB∥DC,AD∥BC B.AB=DC,AD=BC
C.AO=CO,BO=DO D.AB∥DC,AD=BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题提出:用n根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?
问题探究:不妨假设能搭成m种不同的等腰三角形,为探究m与n之间的关系,我们可以从特殊入手,通过试验、观察、类比,最后归纳、猜测得出结论.
探究一:
(1)用3根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?此时,显然能搭成一种等腰三角形.所以,当n=3时,m=1
(2)用4根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?只可分成1根木棒、1根木棒和2根木棒这一种情况,不能搭成三角形,所以,当n=4时,m=0
(3)用5根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?若分成1根木棒、1根木棒和3根木棒,则不能搭成三角形?若分为2根木棒、2根木棒和1根木棒,则能搭成一种等腰三角形,所以,当n=5时,m=1
(4)用6根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?若分成1根木棒、1根木棒和4根木棒,则不能搭成三角形?若分为2根木棒、2根木棒和2根木棒,则能搭成一种等腰三角形,所以,当n=6时,m=1
综上所述,可得表①
n | 3 | 4 | 5 | 6 |
m | 1 | 0 | 1 | 1 |
探究二:
(1)用7根相同的木棒搭成一个三角形,能搭成多少种不同的等腰三角形?(仿照上述探究方法,写出解答过程,并把结果填在表②中)
(2)分别用8根、9根、10根相同的木棒搭成一个三角形,能搭成多少种不同的等腰三角形?(只需把结果填在表②中)
n | 7 | 8 | 9 | 10 |
m |
你不妨分别用11根、12根、13根、14根相同的木棒继续进行探究,…
解决问题:用n根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?
(设n分别等于4k﹣1、4k、4k+1、4k+2,其中k是整数,把结果填在表 ③中)
n | 4k﹣1 | 4k | 4k+1 | 4k+2 |
m |
问题应用:用2016根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?(要求写出解答过程)其中面积最大的等腰三角形每个腰用了 根木棒.(只填结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校准备从体育用品商店一次性购买若干个篮球和足球(每个篮球的价格相同,每个足球的价格相同),购买1个足球和2个篮球共需270元;购买2个足球和3个篮球共需464元.
(1)问足球和篮球的单价各是多少元?
(2)若购买足球和篮球共20个,且购买篮球的个数不超过足球个数的2倍,购买球的总费用不超过1910元,问该学校有哪几种不同的购买方案?哪种方案最省钱?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com